Example27 Sphere Contacting Rigid Wall

General

A sphere contacts a flat rigid wall. The pressure at contact face is analyzed.
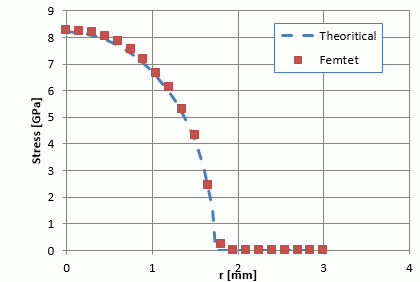
The result matches the Hertz’s theory quite well.
Unless specified in the list below, the default conditions will be applied.

Analysis Space

Item	Settings
Analysis Space	Axisymmetric
Model unit	mm

Analysis Conditions

Axisymmetric analysis is applied on a quarter model.

Item	Settings
Solvers	Mechanical Stress Analysis [Galileo]
Analysis Type	Static analysis
Options	Select none *

* Hertz theory is applied for the minute contact face. Large deformation should not be opted.

Model

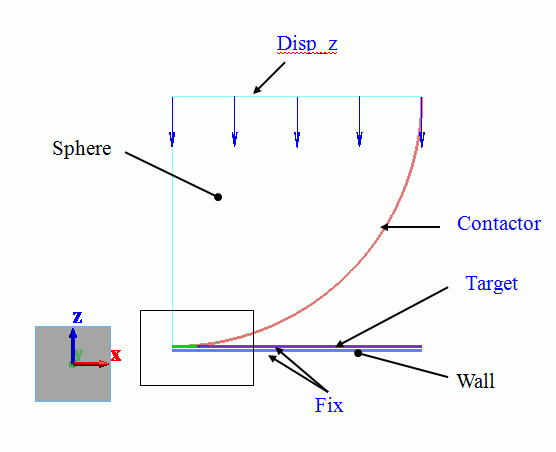
To make the analysis simple, a 2D hemisphere is analyzed. As it is symmetric over Z axis, just a half of the hemisphere is analyzed..

The hemisphere is a sheet body on XZ plane. The upper edge is set with the forced displacement boundary condition.

The top and bottom of Wall are fixed.

The sphere and the rigid plane contact at a point on Z axis

The perimeter of Sphere is “Contactor”. The top of Wall is “Contactee”.

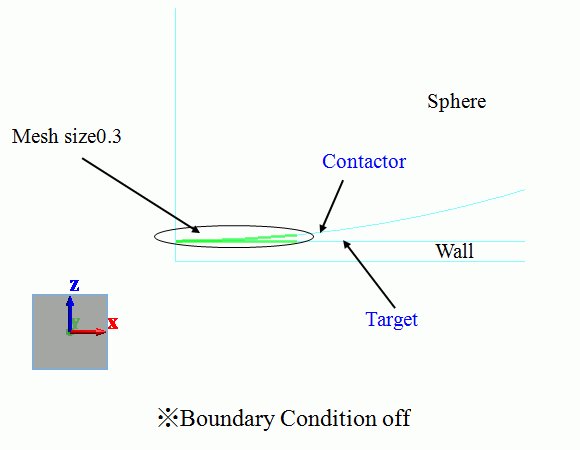
Larger mechanical stresses are expected around the area near the contact point, where

the mesh size is set to 0.3, much finer than the general mesh size of 1.5.

A blown up image is shown below.

Meshing Setup

Setting Item	Item
General Mesh Size	1.5
Meshing Control	Select Place middle nodes on the curve

Middle nodes will make the simulation more accurate.

Body Attributes and Materials

Body Number/Type	Body Attribute Name	Material Name
1/Sheet	Wall	WallMtl
3/Sheet	Sphere	007_Fe *

* Available from the Material DB

The material properties are set up as follows:

Material Name

Tab

Properties

WallMtl

Elasticity

Young’s modulus: 1×10^20[Pa]

Poisson’s ratio: 0

Boundary Conditions

The top edge of Sphere is set with the boundary condition, Disp_z which is -0.1[mm] forced displacement.

Boundary Condition Name/Topology	Tab	Boundary Condition Type	Settings
Fix/Edge	Mechanical	Displacement	Select the XZ component. UX=0, UZ=0
Disp_z/Edge	Mechanical	Displacement	Select the Z component. UZ=1×10^-4[m]
Contactor/Edge	Mechanical	Contact surface	Select “Contactor surface”.
Target/Edge	Mechanical	Contact surface	Select “Contactee surface”.

The contactor and contactee surfaces are designated as a contact pair in the “Boundary Pair” dialog box. In contact analyses, the contact surfaces must be designated as a boundary pair.

Results

The simulation is divided in 20 substeps. The displacement becomes larger gradually in the steps.

20 results are output for the steps between 0.05[Step] and 1[Step].

The number of substeps is 20 by default. It can be adjusted on the Step/Thermal Load tab.

All the results of substeps are output by default. Only final result of 1[Step] can be output too.

The displacement at 1[Step] is shown below.

The contour indicates the Z normal stress. The scale adjustment is “same scale”

[Full Model] is selected to view the other half as well.

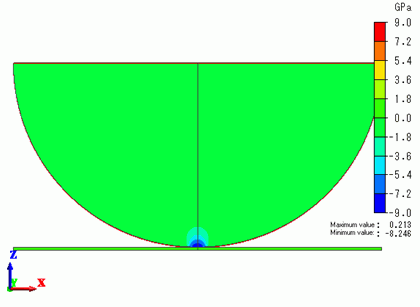
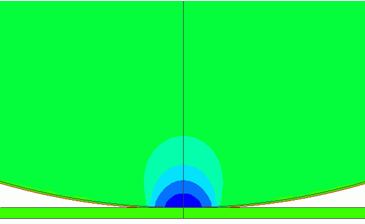
The stresses are concentrating in the contact area.

The contact area is enlarged to show the magnitude of the pressure at the contact face as follows.

The value at the coordinates of contact point (0,0,0) can be shown with [Results at Specified Coordinates].

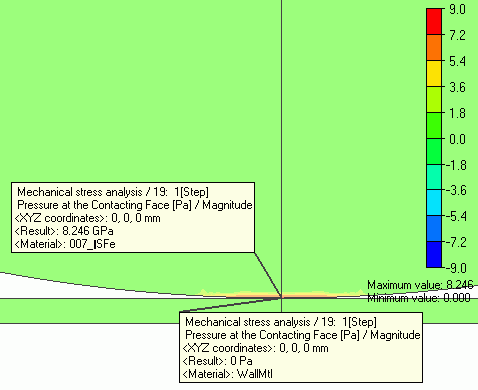
The sphere is crushed around the contact point.

The maximum value of pressure at the contact face is 8.246[GPa]

According to Hertz’s theory,

Total load: F = (16/9*(E/(1-ν^2))^2*R*d^3)^(1/2)

Radius of contactor face: a = (3*F/4*(1-ν^2)/E*R)^(1/3)

The maximum pressure at the contact face: pmax = 3*F/(2*π*a^2)

where E, ν, R and d are Young’s modulus, Poisson’s ratio, radius, and displacement respectively.

For this model, E = 2.06 x 10^11, ν = 0.26, R = 0.03, d = 1.0 x 10^-4.
Therefore, pmax = 8.216[GPa]. It is well matched with the simulation result.

According to Hertz’s theory, the contact area’s pressure is given by the equation below.

p = pmax * (1 – (r/a)^2 )^(1/2)

The chart below indicates that the simulation result and Hertz’s theory match quite well.

See other Stress Analysis examples.