
CAE Software【Femtet】Murata Software Co., Ltd.

Example44 Frictional Contact (#2)
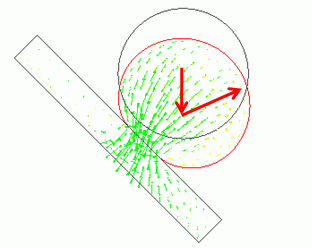
General
-
A ball collides with a plate. The friction is exhibited during the collision..
-
The deformation due to the friction can be observed.
-
Unless specified in the list below, the default conditions will be applied.
Analysis Space
|
Item |
Settings |
|
Analysis Space |
2D |
|
Model unit |
mm |
Analysis Conditions
|
Item |
Settings |
|
Solver |
Mechanical Stress Analysis [Galileo] |
|
Analysis Type |
Transient analysis |
|
Large deformation |
Select “Large displacement”. |
The transient analysis is set up as follows.
|
Tabs |
Setting Item |
Settings |
||||||||
|
Transient analysis |
Table |
|
Model
A polyethylene ball collides with a copper plate whose bottom face is fixed.
The ball has the downward initial velocity, which is set in the body attribute.
Two bodies constitute a boundary pair, on which the coefficient of friction is set.
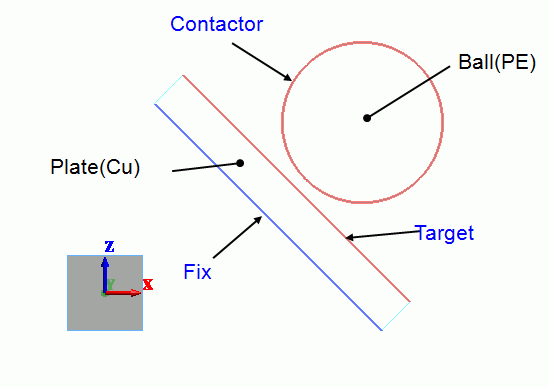
Body Attributes and Materials
|
Body Number/Type |
Body Attribute Name |
Material Name |
|
0/Sheet Body |
Plate |
008_Cu |
|
1/Sheet Body |
Block |
000_Polyethylene(PE) |
The material properties are based on the Material DB.
Boundary Conditions
|
Boundary Condition Name/Topology |
Tab |
Boundary Condition Type |
Settings |
|
Fix/Edge |
Mechanical |
Displacement |
Select the XZ component. UX=0, UZ=0 |
|
Contactor/Edge |
Mechanical |
Contact surface |
Contact Surface Classification: Contactor surface |
|
Target/Edge |
Mechanical |
Contact surface |
Contact Surface Classification: Contactee surface |
The contactor and the contactee constitute a boundary pair. The coefficient of friction is set as follows.
|
Boundary Pair |
Coefficient of Friction |
|
Contactor-Target |
0.4 |
Results
The principal stress distribution at time t=5.0e-5[s] is shown below.

Due to the friction, the compression stresses are inclined in the Z direction with reference to the norm (1, 0, 1).
For comparison, the friction-free model is simulated for the same time duration.
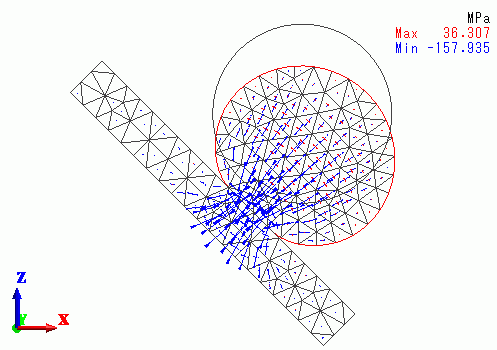
Due to no friction, the stresses are distributed symmetrically with reference to the norm (1, 0, 1).
The traces of the center of the ball are shown below.
It starts at the top left, which is X=0 and z=0.
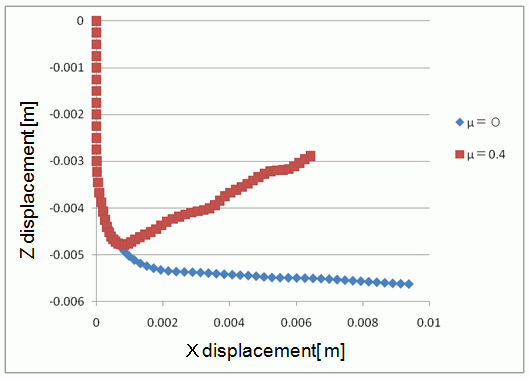
The traces are the same until the ball collides with the plate.
After the collision, the ball bounces in the different directions.
It bounces off horizontally when there is no friction, whereas it bounces back when there is a friction.

