Example61 Resonant Analysis of Beam with Effect of Its Self Weight Taken into Account

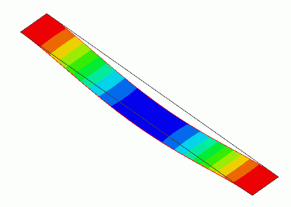
General

The resonant analysis is performed on the beam that is warped due to its self weight in the initial state.
The tensile force is generated in the beam. The resonant frequency is changed due to the warp.
Analysis with the initial stress taken into account is performed. See Analysis with the initial stress taken into account for the details.
Analysis 1 is a static analysis of warp caused by the self weight. The large displacement analysis is used to calculate the warp accurately.
Analysis 2 is a resonant analysis using the results of Analysis 1 as an initial state.
The deformation, the displacement and the mechanical stress are solved.
Unless specified in the list below, the default conditions will be applied.

Analysis Space

Item	Setting
Analysis Space	3D
Model unit	mm

Analysis Conditions

Prepare two analysis models.

The settings of the boundary condition, material property, and body attribute are mostly common for the two models.
Copy an analysis model after setting conditions in the project.

Name Analysis model 1 “Weight_Static” and Analysis model 2 “Resonant”.

Analysis Conditions of Analysis 1

Set up as follows.

Select “Acceleration” at Options to take the self weight into account.

The large displacement is used to calculate the warp accurately.

Item	Setting
Solver	Mechanical stress analysis [Galileo]
Analysis Type	Static analysis
Options	Select “Acceleration”.
Large Deformation	Select Large displacement

The Step/Thermal Load tab is set as follows. The number of substeps is set smaller than the default to shorten the calculation time.

Tab	Setting Item	Setting
Step/Thermal Load	Step/Reached Temperature Setting	Substeps of Step 1 : 5

The Acceleration tab is set as shown below.

Tab	Setting Item	Setting
Acceleration	Acceleration	X=Y=0.0, Z=-9.8[m/s2]

Analysis Conditions of Analysis 2

Set up as follows.

As the analysis is performed using the results of the Analysis 1, select Initial Stress at Options.

Item	Setting
Solver	Mechanical stress analysis [Galileo]
Analysis Space	3D
Analysis Type	Resonant Analysis
Unit	mm
Options	Select Initial Stress (Result Import).

Result Import Tab is set as follows.

Tab	Setting Item	Setting
Result Import	Specify Result	For analysis model, specify [Weight_Static].

Graphical Objects

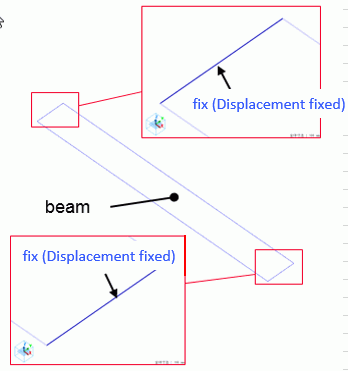
The model is a box solid body. The material is defined.

The fixed displacement boundary condition is set on both ends of the beam.

Set the general mesh size at 0.5.

Body Attributes and Materials

Body Number/Type	Body Attribute Name	Material Name
0/Solid	Beam	Beam

The material properties are set as follows.

Material Name

Tab

Properties

Beam

Elasticity

Young’s modulus: 210×10^9[Pa]

Poisson’s ratio: 0.3

Density

7.8 × 10^3[lg/m3]

Boundary Condition

Boundary Condition Name/Topology

Tab

Boundary Condition Type

Setting

fix/Face

Mechanical

Displacement

Select all X/Y/Z components.

UX=0, UY=0, UZ=0

Results

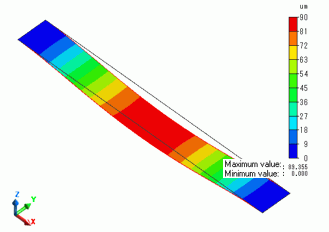
The displacement diagram of Analysis 1 is shown below. The scale factor is 50.
The contour diagram shows the magnitude of displacement.

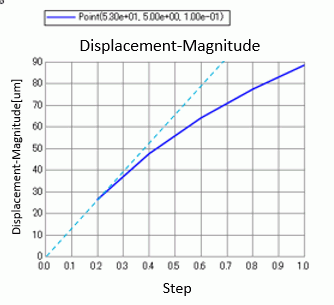
The displacement at the center point(53,5,0.1) varies as shown below. The displacement is not proportional to the steps.
The displacement is restrained as the steps progress.

It indicates that the tensile force is generated in the beam due to the warp.

Large displacement calculation is needed to perform this kind of simulation.

In Analysis 2, vibration component and initial stress component can be displayed.

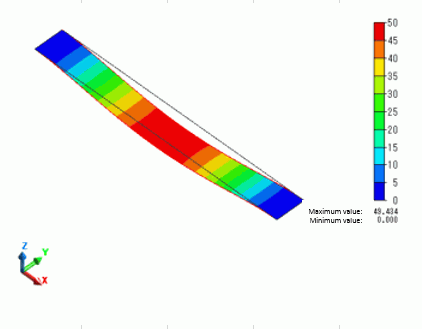
The diagram below shows the first mode of the vibration component. The scale is adjusted automatically.

The same vibration component as in Analysis 1 can be seen.

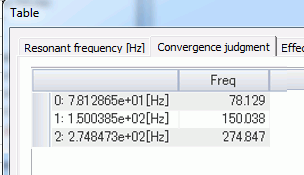
The resonant frequencies are shown in the table below.

By deselcting the option of Initial Stress (Result Import), the resonant frequencies are calculated without taking the warp into account. The following is the result.

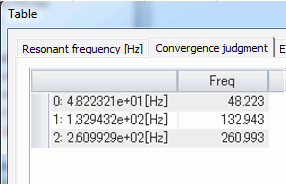
From these two data, you can see the resonant frequencies become higher due to the self weight.

See other Stress Analysis examples.