
CAE Software【Femtet】Murata Software Co., Ltd.

Example33 Coil-to-Coil Power Transfer (Electromotive Calculation)
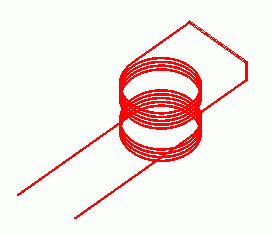
General
-
The power is transferred from the primary coil to the secondary coil.
-
The magnetic field vectors and the electromotive force in the secondary coil are solved.
If you want to solve the transfer power [W], use the electromagnetic waves analysis [Hertz]. ([Example 28: Coil-to-Coil Power Transfer])
-
Unless specified in the list below, the default conditions will be applied.
Analysis Space
|
Item |
Settings |
|
Analysis Space |
3D |
|
Model unit |
mm |
Analysis Conditions
|
Item |
Setting |
|
Solver |
Magnetic Field Analysis [Gauss] |
|
Analysis Type |
Harmonic analysis |
|
Options |
N/A |
The frequency of the current is set to 30[kHz].
|
Tab |
Item |
Setting |
|
Mesh Tab |
Frequency-Dependent Meshing |
Reference frequency: 30×10^3[Hz] |
|
Harmonic analysis |
Sweep Type |
Single frequency |
|
Frequency |
30×10^3[Hz] |
Set the Mesh Tab as follows.
|
Tab |
Item |
Setting |
|
Mesh Tab |
Meshing Setup |
Automatically set the general mesh size: Deselect General mesh size: 2[mm] |
Model
Two coils (Coil1 and Coil2) are placed.
The inflow/outflow faces of the primary coil (Coil1) are extended to the outside of the ambient air. They contact the electric wall of outer boundary condition.
Due to the finite element method, the inflow/outflow faces must be outside of the ambient air to perform the magnetic-harmonic analysis.
In this Exercise, ambient air is set to be created automatically. Therefore, the inflow/outflow faces are extended to the outside of ambient air.
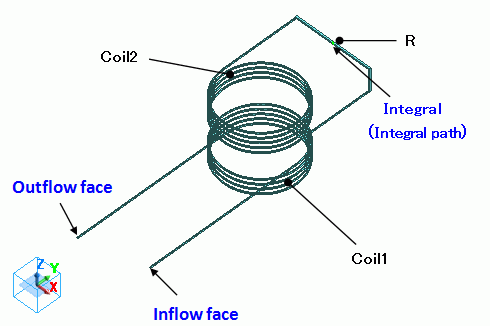
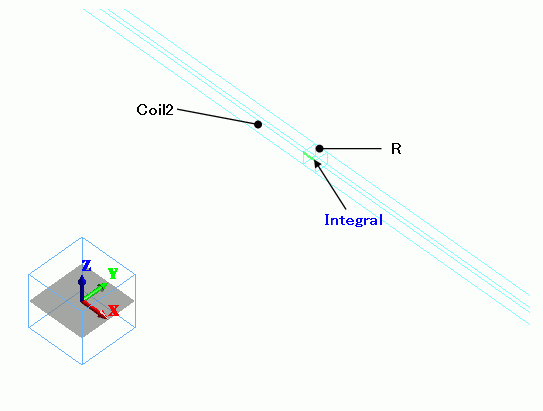
Secondary coil (Coil2) is terminated with R having sufficient resistance value to measure the electromotive force.
If the boundary condition of integral path is set along the current path, the electromotive force can be calculated by integrating the electric field (current density*resistance) on the integral path.
Basically, the body R is not needed when setting the integral path along the current path of the loop coil. However, the current density is not constant at the section of the coil and calculation cannot be done accurately.
By adding the body R having resistance high enough compared to the coil,
the electric potential difference is generated mostly at the body R, and the current density at the section of the body R is almost constant. So the calculation will be accurate.
|
Body Number/Type |
Body Attribute Name |
Material Name |
|
4/Solid |
Coil1 |
008_Cu * |
|
11/Solid |
Coil2 |
008_Cu * |
|
9/Solid |
R |
008_Cu * |
* Available from the Material DB
Body attribute of the primary coil is set up as follows to apply the current.
The setting of the secondary coil is not needed as the current is not applied.
|
Body Attribute Name |
Tab |
Setting |
|
Coil1 |
Current |
Waveform: AC Current: 1[A] Turns: 1[Turns] Direction: Specify Inflow/Outflow Faces Select inflow face and outflow face. |
The electric conductivity of the body R is set low enough compared to the coil as follows.
|
Material Name |
Tab |
Setting |
|
R |
Conductor wall |
Conductivity Type: Conductor |
|
Conductivity: 1[S/m] |
Boundary Conditions
No setting.
Results
To see the electromotive force, go to the [Results] tab

click [Table] ![]() .
.
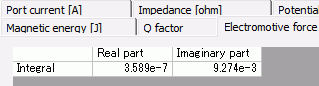
The absolute value is the amplitude of the electromotive force.
About 0.00927[V] is generated in the secondary winding when 1[A] is applied in the primary winding.
The electromotive Ve.m. of the secondary coil is expressed as follows.
Ve.m. = jωM I1
As the frequency is 30kHz, the mutual inductance is 0.491nH (the results of [Mutual inductance calculation project]), and the current I1 at Coil1 is 1A,
amplitude |Ve.m.| of the electromotive force of the secondary coil is calculated to be 0.00925V. This matches with the output result.
-
If you want to solve the transfer power [W], use the electromagnetic waves analysis [Hertz]. ([Example 28: Coil-to-Coil Power Transfer])
The vectors of the magnetic field are shown below.


