Example21 Waveguide Analysis of Balanced Line

General

• The characteristics of a balanced line are analyzed.

• The differential impedance and the propagation constant are solved.

• Unless specified in the list below, the default conditions will be applied.

Analysis Space

Analysis Conditions

* This is the default setting. There are no face electrodes with this model. Therefore it is irrelevant to select it or not.

Mesh tab, Harmonic analysis tab and Open boundary tab are set as follows.

* The general mesh size is a bit too large in this exercise. Smaller mesh size is set.

Model

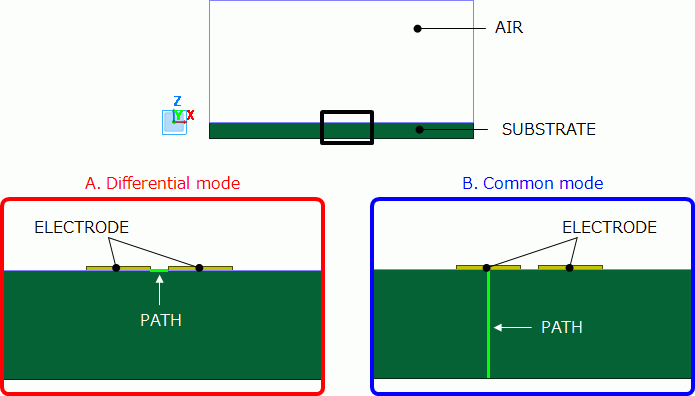
Two electrodes are created on a substrate. They function as a balanced line.
They are covered with rectangle air space.

Setting place of the wire body for integral path (PATH) depends on the mode to analyze.
For the differential mode analysis, place the wire body between the electrodes as in the diagram A.
For the common mode analysis, place the wire body between one of the electrodes and the ground as in the diagram B.

Body Attributes and Materials

* Available from the Material DB

Boundary Conditions

Results

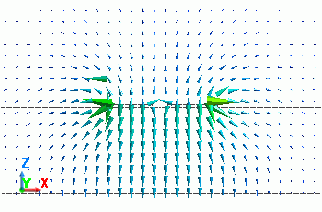
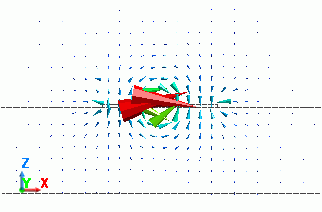
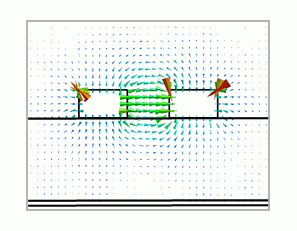
1. Propagation Mode

As the maximum number of the propagation modes is set to 2 in the analysis condition,
two propagation modes are calculated for one frequency.

Regardless of the integral path location, electric fields of two modes are as follows
From the shapes of the electric fields, you can tell that the first mode is the common mode and the second mode is the differential mode.

2. Characteristic Impedance

On the Characteristic impedance (Zpv)[ohm] tab in Table, you can check the characteristic impedance.
The following diagram shows the characteristic impedance obtained for the models with integral path locations A and B above.
Please note that calculation of the characteristic impedance of the common mode is inaccurate if the integral path location A is used which is for the differential mode analysis.
Also, calculation of the characteristic impedance of the differential mode is inaccurate if the integral path location B is used which is for the common mode analysis.

3. Propagation Constant

Unlike characteristic impedance, propagation constant is not affected by the location of integral path.

Propagation constant tab in Table, you can check the propagation constant as follows.
Regardless of the integral path location, the same values are calculated.