Example28 Coil-to-Coil Power Transfer

General

• The self inductances and the mutual inductances are solved for two coils.

• Current flowing in the coil and electromotive force at the secondary coil are calculated.

• Unless specified in the list below, the default conditions will be applied.

Analysis Space

Analysis Conditions

* This is the default setting. It is irrelevant to select it or not as there are no face electrodes with this model.

Harmonic Analysis tab and Open Boundary tab are set as follows.

Graphical Objects

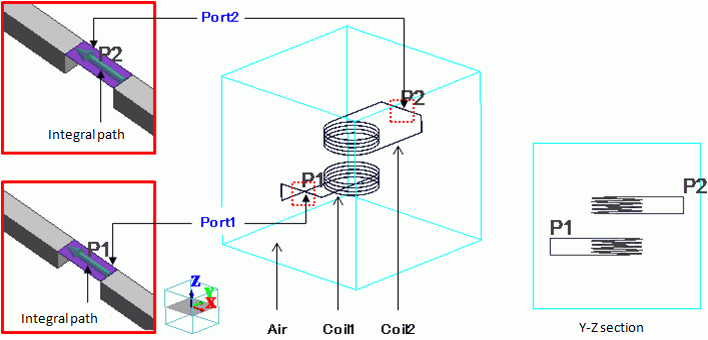
Two coils (Coil1 and Coil2) are placed in a cubic ambient air.
Both ends of each coil are connected by the sheet bodies of I/O ports.
The ports of Coil1 and Coil2 are Port1 and Port2 respectively and the integral paths are set.

• As explained in the Example 33: Coil-to-Coil Power Transfer (Electromotive Calculation) of the magnetic analysis,
  ports of the coils need to be extended to the electric wall. In the electromagnetic analysis, however, such setting is not required.
  The ports can be added connecting the ends of coils in the analysis domain.

Body Attributes and Materials

(*) Available from the Material DB

Boundary Conditions

Result 1: The self inductances and the mutual inductances

Self inductances and a mutual inductance can be calculated through the acquired impedances. They can be compared with the values acquired by magnetic field analysis.

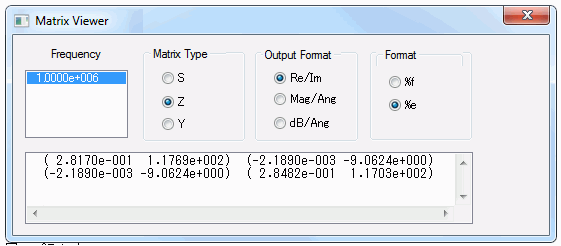
Figure 1: Z-Parameter

In the [Matrix Viewer] dialog box shown above, Re/Im is selected at Output Format.
The value is in the format of (Real part, Imaginary part). Therefore,

Z11 = 0.28664 + 117.69j

is true. The self inductances and the mutual inductance are calculated as follows.
Note that angular frequency ω is 6.28×10⁶rad/s as the frequency is 1MHZ.

L1=18.74[uH] as Z11 = R1+jωL1
L2=18.64[uH] as Z22 = R2+jωL2
M = 1.44[uH] as Z12 = R3+jωM

The self inductances and the mutual inductances given by the analysis are as follows.
(Acquire the project file for the magnetic field analysis) (Save the project file before open)

L1 = 19.63[μH]
L2 = 19.63[μH]
M = 1.47[uH]

The difference is only 2 to 5 %.

• To show the [Matrix Viewer] dialog box, go to the [Results] tab and in [Chart] , select [SYZ Matrix].
  In the [SYZ Matrix] dialog box, select [Matrix Viewer] from the [View] menu.

Result 2: Transferred power

The transferred power Pout[W] when the power Pin[W] is applied at the primary Coil1
is obtained by the following two methods.

1. S-Parameter Method

The transferred power Pout is calculated with input power Pin and S-parameters S21 as follows.

Pout = Pin ×|S21|²

In this example, Pin is 1.0W on the [Harmonic analysis] tab.
S-parameters are calculated as in the Figure 2 below.

|S21|² = (-0.0405)² + 0.0383² = 0.00311

Pout is 3.1mW.

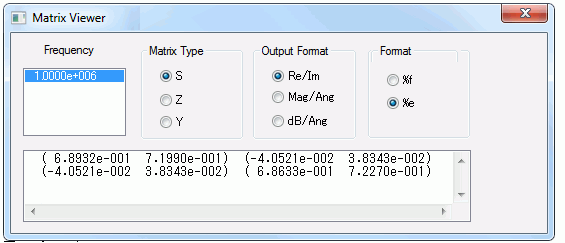
Figure 2: S-parameters

2. Voltage Method

Transferred power Pout is calculated with the amplitude of power V2[V] on the Coil2
and the reference impedance Z[Ω] of the port.

Pout = |V2|²/(2Z)

To calculate the amplitude of voltage at the port, select X component of the electric field as it is parallel with the integral path of Port2.
For [Phase], select Absolute and integrate on the integral path. (Figure 3)

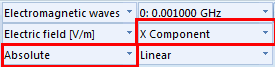
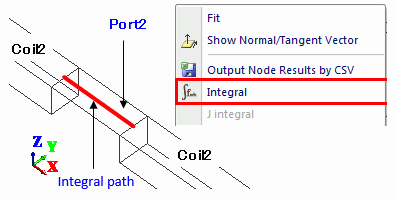
Figure 3: Calculation of voltage at port

In this example, the output window below will show up after the integral command execution as follows.
The amplitude of voltage is 0.558V.

Reference impedance is 50Ω which is the reference impedance of Port2.
Transferred power is 3.1mW.

Result 3: Current in the coil

If the frequency goes higher, the current tends to concentrate on the surface of coil and current density distribution will be generated on the section of coil.
Therefore, accurate value of current cannot be given by the calculation where the current density at a point on the section is multiplied by the section area.
Current in the coil is calculated with the Ohm’s law I=V/R ( I: current [A], V: voltage [V], R: resistance [Ω])
and the voltage applied to the resistor on the coil.
As an example, Current I1 in the Coil1 is calculated here.

First, place resistor on Coil1.
As shown in the Figure 4, remove a part of Coil1 and connect with a sheet body.
Set lumped-constant boundary condition on the sheet body. Resistance is 1Ω

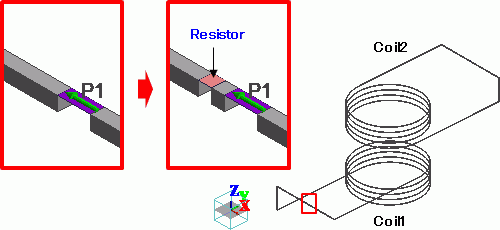
Figure 4: Remove a part of coil and place resistor sheet body

Execute the integral command on the electric field to calculate the voltage applied to the resistor.
In this example, electric field vector is in the X direction at the resistor.
Select X Component for the [Component] of electric field. Select Absolute for [Phase] to calculate the amplitude of voltage at the resistor.
As in the Figure 5, select an edge of the resistor sheet body parallel with the electric field and execute the integral command.
Then the output window will appear showing the voltage at the resistor as integral results.
In the Ohm’s law, I = V/R. As R is now 1 [Ω], the value of voltage represents the value of current.

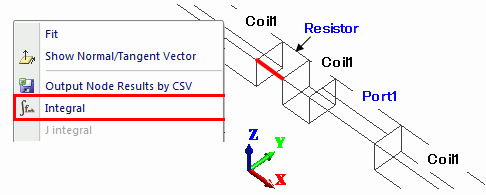
Figure 5: Calculation of current in the coil

For easy understanding, type of Port1 is changed from the power port to the current port.
The current at Coil1 is calculated with resistor of 1Ω on the coil.
The output window below will show up after the integral command execution as follows.
The amplitude of current is 1A.

• The current with amplitude of 1A flows in the current port.
  See [I/O Port of Electromagnetic Analysis] for more details.

Type of Port1 is switched back to the power port and perform the analysis.
The output window below will show up after the integral command execution as follows.
If the power with amplitude of 1W is applied to Coil1, the current with amplitude of 0.16A will flow.

Result 4: Electromotive force of secondary coil

Setting Coil1 as the primary coil, the electromotive force of the secondary Coil2 is calculated.

To make open ends of Coil2, remove the sheet body Port2.
In order to execute the integral command after the analysis,
place air body between the ends of Coil2 as in the Figure 6.

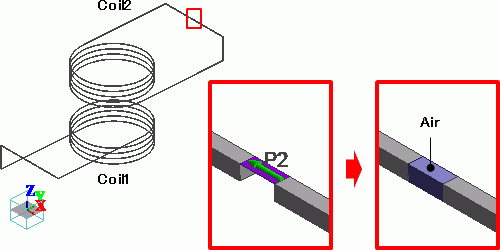
Figure 6: Remove port and place air body

Perform analysis and calculate the electromotive force of Coil2.
In this example, electric field vector is in the X direction (from one end to another) between the ends of Coil2.
Select X Component for the [Component] of electric field. Select Absolute for [Phase] to calculate the amplitude of electromotive force.
As in the Figure 7, select an edge of the air body parallel with the electric field and execute the integral command.
Then the output window will appear showing the electromotive force as integral results.

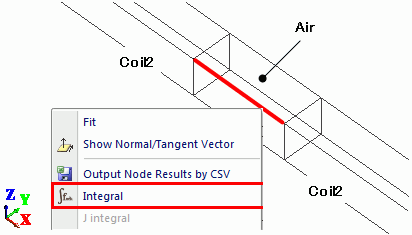
Figure 7: Calculation of electromotive force

In this example, the results are shown on the output window as follows.
The amplitude of electromotive force is about 1.4V.

The electromotive V_e.m. of the secondary coil is expressed as follows.

V_e.m. = jωM I1

The angular frequency ω is 6.28×10⁶rad/s, and the mutual inductance M is 1.44μH as per Result 1 in this example.
The amplitude of current in the Coil1 is 0.16A as per Result 3 in this example.
The amplitude |V_e.m.| of the electromotive force of the secondary coil is about 1.4V.
This matches with the integral results on the output window.