例題48

座屈解析の事例

解析の種類として座屈解析を選択しています。

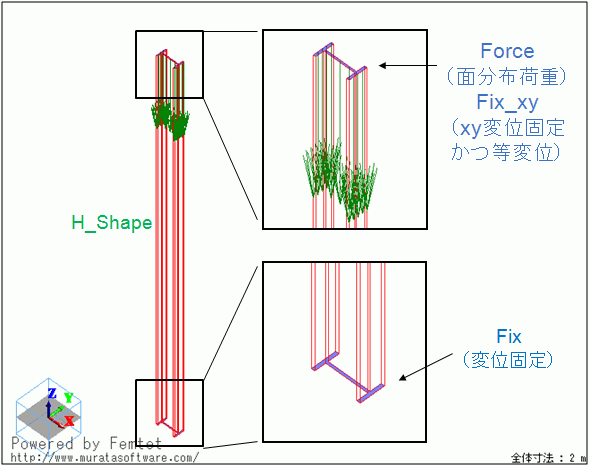
まず、XY平面上にH型のシートボディを作成し、Z方向に引き延ばし加工することで柱形状のソリッドボディを形成しています。
底面の変位を固定し、上面に下向きの荷重およびXY方向の変位固定（＋等変位※）を設定しています。

※等変位チェックをすることで上面の回転変位を抑制しています。

ボディ No./ボディタイプ	ボディ属性名	材料名
0/Solid	H_shape	104_ステンレス鋼※

※材料データベースを利用

境界条件名/トポロジ	タブ	境界条件の種類	条件
Fix/Face	機械	変位	XYZ成分のチェックボックスをオン UX=0, UY=0, UZ=0
Force/Face	機械	荷重	トータル荷重で入力するのチェックボックスをオン X=0.0, Y=0.0, Z=-1000
Fix_xy/Face	機械	変位	XY成分のチェックボックスをオン UX=0, UY=0 等変位チェックをオン等変位UX, UY, UZのチェックをオン

計算値ファイルには以下のような解析結果が出力されます。

<<座屈解析>>

座屈荷重係数(Buckling Load Factor)

Mode[ 0] = 2.88264161e+002

モデルに設定された荷重に座屈荷重係数を乗算したものが座屈荷重となります。

応力座屈解析で得られるフィールド値（変位、ひずみ、応力など）はすべて相対値です。

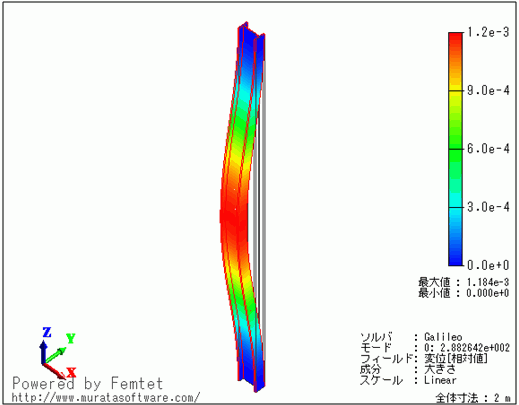
上の結果より、本モデルでの座屈荷重係数が288であることが分かります。

したがって、境界条件Forceで設定した荷重は1000[N]ですので、座屈荷重は288[kN]となります。

変形図を示します。コンター図は変位の大きさを示してます。変位量の相対値です。

断面形状がＨ型の柱の座屈荷重は以下の理論公式から求められます。

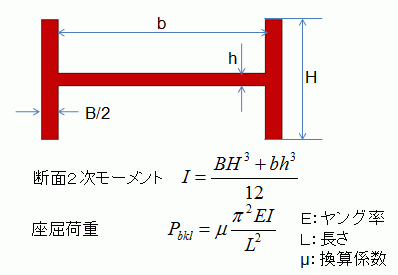
本例題の場合、

B/2 = 7e-3[m]

b = 86e-3[m]

H = 50e-3[m]

h = 5e-3[m]

E = 2e11[Pa]

L = 2.0[m]

μ＝4（両端の水平変位および回転変位が固定のため）

であるので　I = 14.7e-8[m4]、Pbkl = 290[kN]

となり、Ｆｅｍｔｅｔの座屈荷重解析結果とよく一致しています。