片持ち梁のエアダンピング

本例題について

• 小さな片持ち梁の空気抵抗による減衰を考慮した解析を行い、基本モードの減衰比（=1/（2*Q値））を求めました。減衰は音響インピーダンスの境界条件で与えますが、その値は、流体中の球に加わる抗力から推測した値を使いました。

• 解析で得られた減衰比を、参考文献に掲載された実験値と比較し、２割ほどの差で一致することを確認しました。

• 圧電性を無視して計算を行いました。
   

• 表に記載されていない条件は初期設定の条件を使用します。

解析条件

共振解析タブ

モデル図

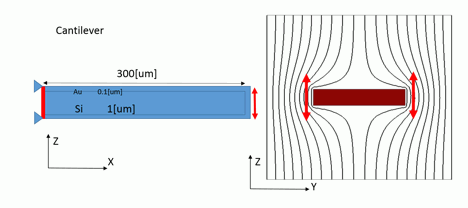
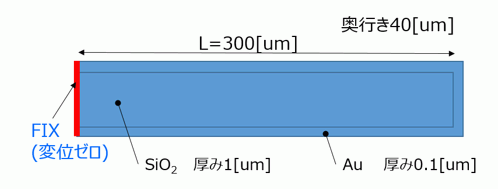
SiO2の片持ち梁（300ｘ40ｘ1[um]）の周りに厚さ0.1[um]のAu層を構成した構造になります。梁の長さ(L)を 300、250、200、150[um]と変えて、解析を行いました。

BODY属性および材料定数の設定

境界条件

(*)zre,zimは入力しやすいよう、変数で定義しています。

エアダンピングを考慮した解析を行うため、音響インピーダンス（Z）を適切な値に設定する事が必要です。

空気による抵抗と同等の効果を示す音響インピーダンス値を決める方法として、解析結果が実験結果と合うように音響インピーダンス値を決めるという方法が考えられます。しかし、ここでは実験結果が無い場合にも妥当な解析ができるよう、計算で音響インピーダンスの値を決める方法を考えました。

梁の音響インピーダンスを直接的に計算する方法は分かりませんので、近似的な方法を使いました。空気中で、微小な振幅で調和振動する球に加わる力（F)は、理論的に求められます[1]。ここでは文献[2]に示された式(1)を示します。

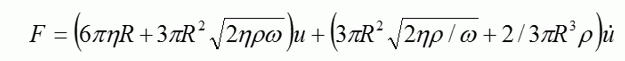 　(1)

 R：球の半径　　ω：角周波数    u：速度　　η：空気の粘性率 = 1.81e-5[Pa･s]　　　ρ：空気の密度=  1.18[kg/m3]

この式を用いて、球と同じ半径（R)をもつ円板が、球と同じ速度で振動する時に、球と同じ力を空気から受けるよう、音響インピーダンスを決めることにします(図１)。音響インピーダンスの境界条件に入力する値（Z)は、Z=圧力/速度、です。この圧力は、(1)式の力を円板の表面積（2πR2）で割って求めます。円板の表面と裏面を考え、側面の影響は無視しています。この考え方により、音響インピーダンスは(2)式で求めることができます。ただし、調和振動を仮定しているので、加速度は du/dt=jωu と書くことができます。

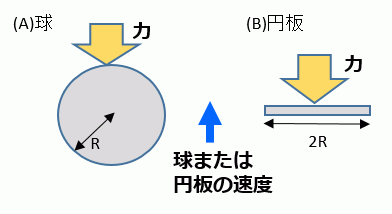
　図１．(A)振動して空気から力を受ける球。(B)振動して空気から力を受ける円板。

　　　　球が受ける力と同じ力を受けるように、円板の音響インピーダンスを決める。

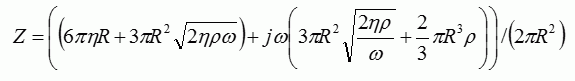  (2)

梁の奥行き(b)と等しい直径を持つ球を考え、音響インピーダンスを（2）式で求めることにします。

(2)式を計算するためには角周波数が必要なので、まず音響インピーダンス（Z)を設定しない状態（Z=0）で、共振解析を行い、角周波数を求めます。下の表では、このようにして共振周波数を求め、

(2)式で音響インピーダンス（Z）を求めました。梁の奥行きは40μmなので、R=20μmとして計算しています。

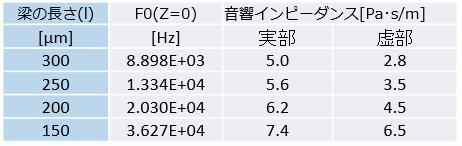
表１のf0[Hz]を解析条件、共振解析タブ、周波数の近似値に入力します。その周波数で求めた音響インピーダンスの値を外部境界条件に設定し、解析すると、複素共振周波数が求められます。

複素共振周波数から、減衰比、Q値を求めることが可能です。

• 解析１．添付のプロジェクトファイルをそのまま実行します。この状態は梁の長さ(l)を300[um]です。
• 結果１．共振周波数（実部のみ）が得られます。（表１のｆ０が得られます。）
• 解析２．ｆ０を（解析条件、共振解析タブ）周波数の近似値に、音響インピーダンスZを境界条件に入力し、解析します。
• 結果２．複素共振周波数が得られます。複素共振周波数から、減衰比、Q値を求めることが可能です。
• 添付のプロジェクトファイルは、梁の長さ(l)を300[um]、音響インピーダンス（Z)を０[Pa・s/m]に設定しています。これらは変数として定義していますので、変更は容易です。

解析結果

結果の図を示します。

片持ち梁の基本振動モードが確認できます。コンター図の色は変位の大きさに対応しています。

結果として得られた複素共振周波数（f0）を表に示しました。　減衰比は、f0の実部と虚部の比として求め、文献[3]に掲載された実験値と比較を行いました。

表の右端の列を見てください。減衰比の計算値と実験値の比を示しています。この結果、２割以内の誤差で一致していることが分かりました。

参考までに、減衰比(ζ)、Q値、複素共振周波数(f0=fre+j fim)の関係を示します。

参考文献

[1]　ランダウ＝リフシッツ　流体力学１。

[2]  国分清秀、平田正紘、小野雅敏、村上寛、戸田義継：真空　30　（1987）　714

[3]　Christian Bergaud, Liviu Nicu and Augustin Martinez 　：　Multi-Mode air damping analysis of composite cantilever beam ,Jpn.J.Appl.Phys., 38,(1999)6521