接触面圧力の解析

本例題について

• 球体が剛体平面に接触した際の接触面圧力を解析した例を示します。

• Femtetの結果とヘルツの公式による理論値が良く一致することを示します。

• 表に記載されていない条件は初期設定の条件を使用します。

解析空間

解析条件

形状の対称性を利用して軸対称モデルを解析します。

(*)Hertzの公式は物体の表面に比較して接触面が微小である前提となってますので、大変位オプションには

チェックせず、微小変形の範囲で比較します。

モデル図

対称軸をZ軸、半径方向をX軸として軸対称のモデル形状を作成しています。

半径30mmの球体（Sphere)の下半分のシートボディを作成し上側の面にZ方向の強制変位を設定しています。

剛体平面（Wall)は変形させないため上下面の変位を固定しています。

球体と剛体平面のシートボディはあらかじめ対称軸(Z軸）上で点接触させています。

球体と剛体平面の接する予定の面（モデル形状では辺）にそれぞれ接触面と被接触面を設定しています。

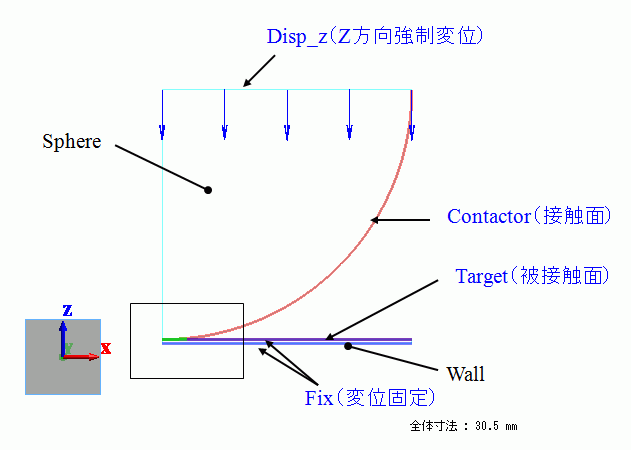
特に上の図で黄色の四角形で囲んだ対称軸（Z軸）上の接触点付近には局所的に応力が発生することが予想できますので

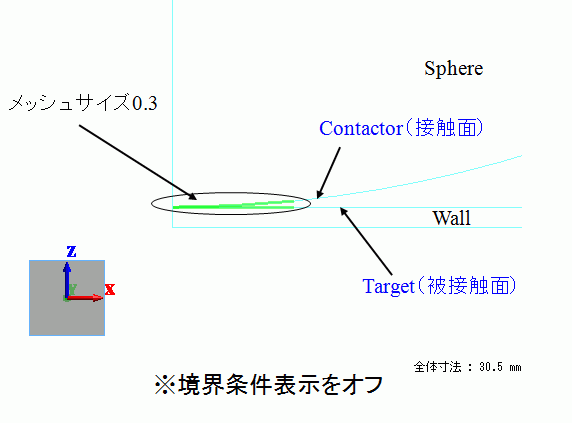
球体、剛体平面ぞれぞれのボディにX=3mmにて辺を刻み、標準メッシュサイズ1.5よりも小さめのメッシュサイズ0.3を設定しています。

以下に接触点付近の拡大図を示します。

メッシュ設定

曲面形状のモデルの接触解析では接触面の形状ができるだけ理想に近い方が望ましいためチェックしています。

ボディ属性および材料の設定

※材料データベースを利用

材料定数は以下のように設定しています。

境界条件

半径30mmの球に対して微小変位として0.1mmのZ軸マイナス方向の変位（Disp_z)を設定しています。

ContactorとTargetはお互いが接触しあう接触表面のため境界条件のペア設定を行っています。

解析結果

接触解析では、指定の変位に到達するまでの過程を20分割して、徐々に変位を大きくしながら計算を行っています。

0.05[Step]～1[Step]まで、20個の解析結果が出力されます。

初期条件では分割数は20が設定されていますが、ステップ/熱荷重タブで変更することができます。

初期条件では分割ステップすべての結果が出力されますが、最終的な1[Step]の結果のみ出力することも可能です。

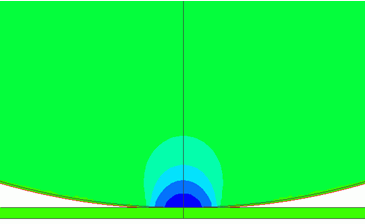
1[Step]での変形図を示します。

カラーコンターは応力のZ垂直応力を示してます。変形図の倍率は等倍としています。

コンター図の最小値と最大値は、-9G、9Gに設定しています。

軸対称モデルの左半分も表示させるために、「対称モデルの全体モデル表示」を行っています。

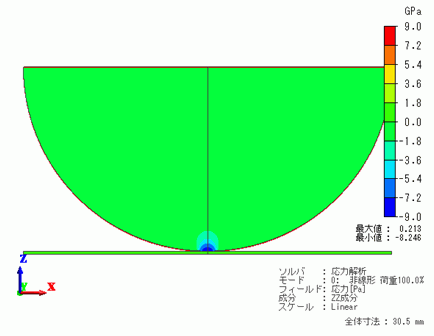
接触部に応力が集中して発生していることが分かります。

次に、接触部の拡大し、接触面圧の大きさを表示します。

接触箇所の座標(0,0,0)の値を「任意座標の計算結果」により、表示しています。

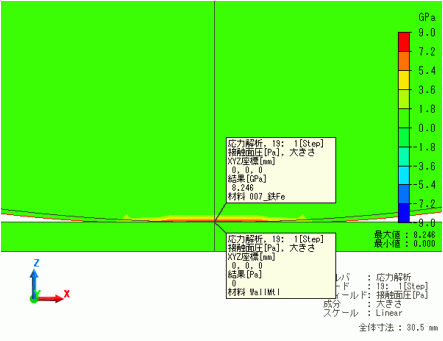
接触部においては球面と剛体平面同士が面接触していることが分かります。

解析結果より接触面における最大接触面圧力は8.246[GPa]であることが分かります。

ヘルツの公式による理論値は以下の式で算出されます。

トータル荷重：　F = (16/9*(E/(1-nu^2))^2*R*d^3)^(1/2)

接触面半径：　a = (3*F/4*(1-nu^2)/E*R)^(1/3)

最大接触面圧力：　pmax = 3*F/(2*pi*a^2)

ここでE、nu、R、d　はそれぞれ球体のヤング率[Pa]、ポアソン比、半径[m]、変位[m]です。

今回のモデル条件（E = 2.06 x 10^11, nu = 0.26, R = 0.03, d = 1.0 x 10^-4 ）では
pmax = 8.216[GPa] となり、Femtetによる結果 8.246[GPa]と良く一致しています。

さらにヘルツの公式によると中心軸からの距離ｒ にたいする接触面圧ｐは

p = pmax * (1 – (r/a)^2 )^(1/2)

とされており、この公式とFemtetの解析結果から得た面圧力分布を比較した結果を以下に示します。

辺に沿った応力の数値は、辺を選択して、右クリックメニューから「節点結果のcsv出力」で取得できます。

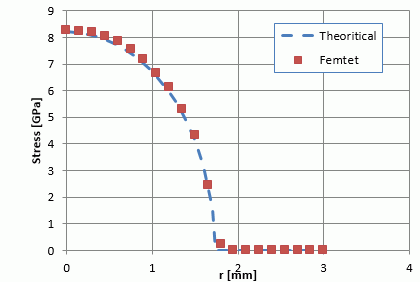
接触面領域全域にわたってFemtetによる解析結果とヘルツの公式による理論値が良く一致していることが分かります。

参考文献：

「有限要素法による構造解析事例集」　サイエンス社

機械工学便覧 A4 材料力学　日本機械学会編