エネルギー解放率

本例題について

• 亀裂の入った板を引っ張た時の応力を解析します。

• 計算の結果得られたひずみエネルギーからエネルギー解放率と応力拡大係数を計算します。
  これらの値は破壊強度を評価する時に使用します。

• 同様の解析を異なる方法で解析した例題４６ J積分を用いた亀裂先端のエネルギー解放率解析も
  参考にしてください。

• 表に記載されていない条件は初期設定の条件を使用します。

解析空間

解析条件

モデル図

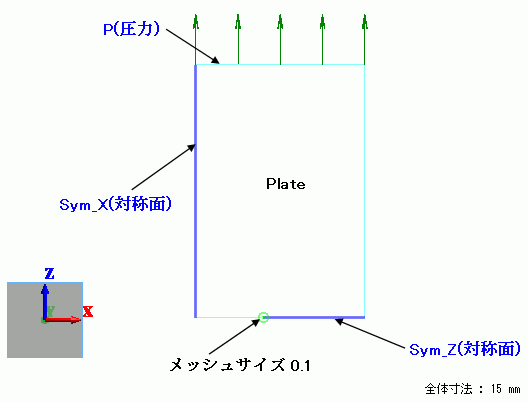
下図のように中央に亀裂が入った板を引っ張ったときの応力を計算します。

強く引っ張った時に、先端から破壊されますが、この時の破壊強度を評価

するのに応力拡大係数Kが使用されます。このモデルの場合のKは、次式の

理論解が知られています。

この応力拡大係数を、Femtetを使って計算してみます。

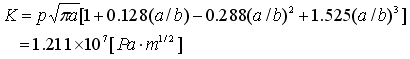
出展）

鷲津久一郎他、有限要素法ハンドブックⅡ応用編、培風館, p.329

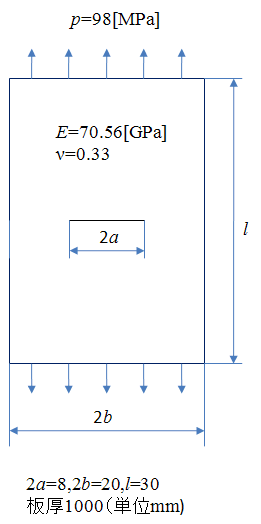
モデルは左右上下対称なので、右上の1/4領域だけを解析します。

対称面には、「対称/不連続タブ」で「対称面」を設定します。

ただし、亀裂面は開放状態であるため、対称面を設定する必要はありません。

BODY属性および材料定数の設定

ボディ属性で、シートボディの厚みを1mにします

材料定数で、ヤング率とポアソン比を設定します

※材料定数は、上記記載の出典で使用しているヤング率とポアソン比を設定しています。

境界条件

解析結果

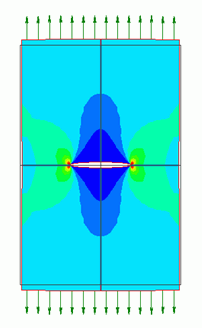
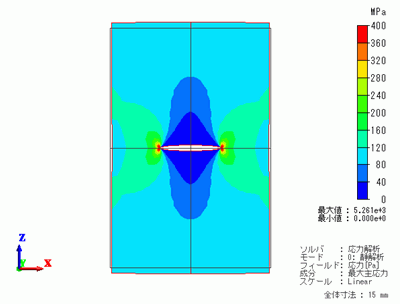
変形図に応力の最大主応を重ねた図を示します。

コンター図の表示範囲を0～400MPaに設定しています。

対称面境界を設定しているので、全体モデルが表示されています。

亀裂の先端に強い応力が発生していることがわかります。

エネルギー解放率

亀裂先端の応力は、理論的には無限大ですが、実際には大きい値になっており、その値は

メッシュ分割によって敏感に変化します。したがって、ここの応力の値で破壊強度を評価する

ことはできません。破壊強度の評価には、エネルギー解放率gや応力拡大係数Kなどが使用

され、その値の大小で破壊強度を評価します。

エネルギー解放率gは、ひずみエネルギーUと亀裂の長さaの変化率で次式で定義されます。

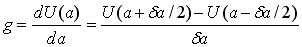                       (1)

ここではaの変化を0.1mmとし、a=4.05とa=3.95の場合のひずみエネルギーを計算します。

上の1/4モデルで、a=4.05[mm]のとき、U=12.1805977[J]、a=3.95のとき、

12.0728236であるので、全体モデルでは

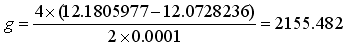              (2)

分子に４をかけたのは、全体モデルのエネルギーは1/４モデルの４倍になるからです。

また、分母に２をかけたのは、全体モデルで亀裂の長さは２倍変化するからです。

応力拡大係数

２次元の場合は、エネルギー解放率gと応力拡大係数Kとは次の関係があります。

平面応力

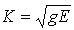                                                                                   (3)

平面ひずみ

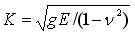                                                                    (4)

今回の場合、平面応力なので式(3)を使用し、式(2)の結果から応力拡大係数は

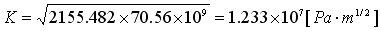      (5)

この値は、冒頭の理論解と2％程度の差で一致しています。