コイル間の電力伝送

本例題について

• 二つのコイルの自己インダクタンス、相互インダクタンスを求めています。

• コイルに流れる電流や2次側コイルの起電力を求めることができます。

• 表に記載されていない条件は初期設定の条件を使用します。

解析空間

解析条件

※本オプションは初期設定条件ですでにチェックが入っています。本例題では面電極は

　ありませんので、チェックがなくても結果には影響しません。

調和解析および開放境界の設定を以下のように行っています。

モデル図

2つのコイル（Coil1、Coil2）を立方体の空気領域の中に設置しています。
Coil1、Coil2それぞれの両端は、空気領域内部で入出力ポートを設定したシートボディでつないでいます。
Coil1のポートを“Port1”、Coil2のポートを“Port2”とし、それぞれに積分路を設定しています。

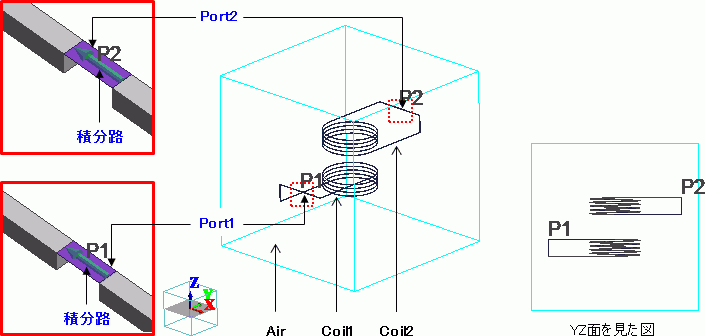
• 「磁場解析例題33 コイル間の電力伝送（起電力計算）」にあるように、磁場解析の調和解析では
  コイルのポートは電気壁まで引き出す必要がありますが、電磁波解析ではその必要がありません。
  本例題のように、解析領域内でコイルの両端をつなぐようにポートをつけることができます。

ボディ属性および材料定数の設定

※材料データベースを利用

境界条件

解析結果1： 自己インダクタンス・相互インダクタンス

インピーダンスから自己インダクタンス、相互インダクタンスを求め、磁場解析との一致を確認します。

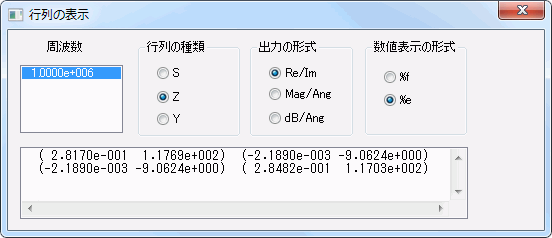
図1 Zパラメータ

上の図1に示した[行列の表示]ダイアログでは、出力の形式でRe/Imを選択しているので、
（実部　虚部）の表示が行われています。つまり

Z11 = 0.28664 + 117.69j

の意味になります。これらの情報から、自己インダクタンス、相互インダクタンスを求めます。
周波数1MHzより、角周波数ωは6.28×10⁶rad/sであることに注意すると、

R1 + jωL1 = Z11 より、L1 = 18.74[μH]
R2 + jωL2 = Z22 より、L2 = 18.64[μH]
R3 + jωM = Z12 より、M = 1.44[μH]

磁場解析の結果で得られた自己インダクタンス、相互インダクタンスは、次の通りです。
（磁場解析プロジェクトはこちら）（保存してから開いてください。）

L1 = 19.63[μH]
L2 = 19.63[μH]
M = 1.47[μH]

2～5%の差で一致している事が確認できました。

• [行列の表示]ダイアログを表示するには、[解析結果]タブの[チャート] から[SYZ行列]を実行し、
  [SYZ行列]ダイアログの[表示]メニューからから[行列の表示]を実行します。

解析結果2： 伝送電力

1次側コイルCoil1にPin[W]入力したときの伝送電力Pout[W]は、
次の2つの方法で求められます。

1. Sパラメータを用いた方法

伝送電力Poutは、入力電力PinとSパラメータS21を用いて、次式で得られます。

         Pout = Pin ×|S21|²

本例題では、Pinは解析条件の[調和解析]タブで1.0Wと設定しています。
また、Sパラメータは下の図2のように計算されているので、

         |S21|² = (-0.0405)² + 0.0383² = 0.00311

より、伝送電力Poutは3.1mWと計算できます。

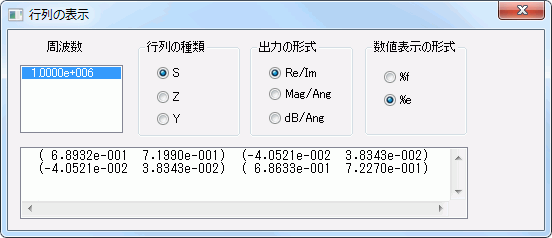
図2 Sパラメータ

2. ポートに生じる電圧を用いた方法

伝送電力Poutは、2次側コイルCoil2のポートに生じる電圧V2[V]の振幅と
ポートの基準インピーダンスZ[Ω]を用いて、次のように計算することができます。

         Pout = |V2|²/(2Z)

ポートに生じる電圧の振幅Vは、Port2の積分路がX成分に平行なので電界のX成分を表示し、
[位相]コンボボックスをAbsoluteにして積分路上で積分コマンドすることで計算できます（図3）。

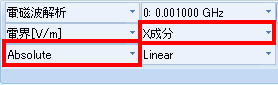
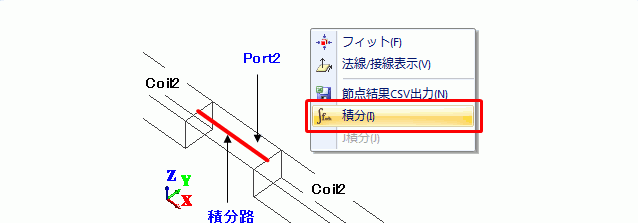
図3 ポートに生じる電圧の求め方

本例題では、積分コマンドを実行すると出力ウィンドウに次のように表示され、
電圧の振幅は0.558Vということが分かります。

基準インピーダンスはPort2の基準インピーダンスとして設定した50Ωなので、
伝送電力は3.1mWと計算できます。

解析結果3： コイルに流れる電流

周波数が高くなると、電流はコイルの表面に集中するようになり、コイル断面に電流密度の分布が生じます。
そのため、コイル断面のある1点の電流密度に断面積をかける計算では、正確な電流値を求められません。
コイルに流れる電流は、オームの法則 I = V/R（I： 電流[A]、V： 電圧[V]、R： 抵抗[Ω]）を用いて、
コイル上の抵抗に加わる電圧から計算します。
ここでは、例としてCoil1に流れる電流 I1 の調べ方を説明します。

まず、Coil1に抵抗を設置します。
図4のように、Coil1の一部を削除し、シートボディでつなぎます。
シートボディには、集中定数の境界条件を設定し、1Ωの抵抗とします。

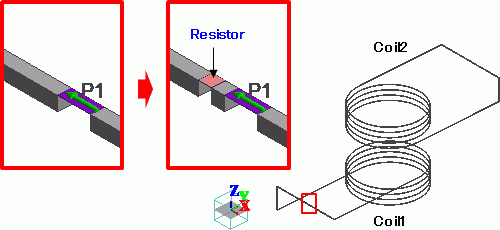
図4 コイルの一部を削除してシートボディの抵抗を取り付ける

解析を実行し、抵抗に加わる電圧を調べるために、積分コマンドを用いて電界を積分します。
本例題で抵抗を付けた場所で電界ベクトルはX方向を向いているので、
電界の[成分]をX成分にし、抵抗に加わる電圧の振幅を計算するために[位相]をAbsoluteにします。
図5のように、電界に平行な抵抗のシートボディの1辺を選択して積分コマンドを実行すると、
出力ウィンドウに積分結果として抵抗に加わる電圧が表示されます。
オームの法則より I = V/R ですが、いま R = 1 [Ω] なので、表示された電圧値がそのまま電流値を表します。

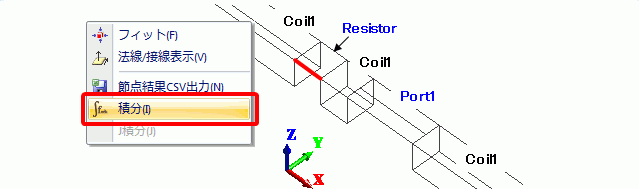
図5 コイルに流れる電流の調べ方

わかりやすいようにPort1のポートの種類を電力ポートから電流ポートに変更し、
Coil1に1Ωの抵抗を付けて解析を行い、Coil1に流れる電流を調べました。
積分コマンドを実行したところ、出力ウィンドウには下のように表示され、
振幅1Aの電流が流れていることがわかります。

• 電流ポートは、振幅1Aの電流が流れるポートです。
  ポートの種類について詳しくは、「電磁波解析の入出力ポート」をご覧ください。

Port1のポートの種類を電力ポートに戻して解析を実行し、Coil1に流れる電流を調べます。
積分コマンドを実行したところ、出力ウィンドウには下のように表示されました。
ここから、Coil1に振幅1Wの電力を入力すると、振幅0.16Aの電流が流れることが分かります。

解析結果4： 2次側コイルの起電力

Coil1を1次側コイルとし、2次側コイルCoil2に生じる起電力を計算します。

Coil2の両端をオープンとするために、Port2のシートボディを削除します。
解析実行後に積分コマンドを実行するために、
図6のようにCoil2の両端の間に空気ボディを挟みます。

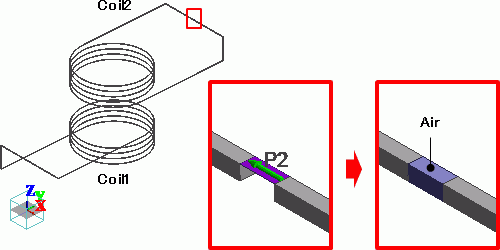
図6 ポートを削除して空気ボディを挟む

解析を実行し、Coil2の起電力を調べます。
本例題では、Coil2の両端間で電界ベクトルはX方向（一端からもう一端へ向かう方向）を向いているので、
電界の[成分]をX成分にし、起電力の振幅を計算するために[位相]をAbsoluteにします。
図7のように、電界に平行な空気ボディの1辺を選択して積分コマンドを実行すると、
出力ウィンドウに積分結果として起電力が表示されます。

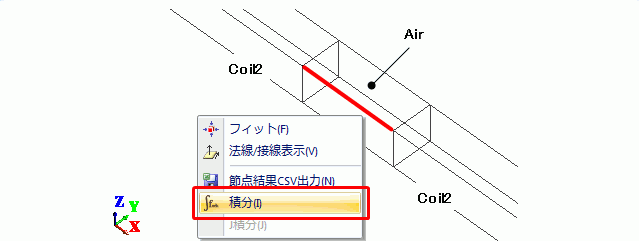
図7 起電力の調べ方

本例題では、出力ウィンドウに次のように表示されました。
ここから、起電力は約1.4Vということが分かります。

2次側コイルの起電力V_e.m.は、次の式で表せます。

         V_e.m. = jωM I1

いま、角周波数ωは6.28×10⁶rad/s、相互インダクタンスMは本例題の解析結果1より1.44μH、
Coil1に流れる電流 I1 の振幅は本例題の解析結果3より0.16Aなので、
2次側コイルの起電力の振幅 |V_e.m.| は約1.4Vと計算できます。
これは、出力ウィンドウに表示された積分結果とよく一致しています。