張力の影響

本例題について

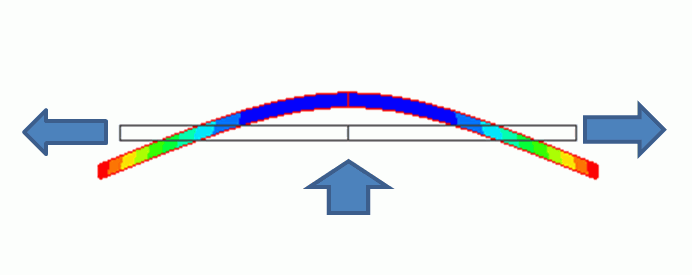
• 張力の影響により硬くなる効果を解析します。上の図をご覧ください。梁を左右に引っ張って、同時に下から押しています。左右に引っ張る力が大きくなると、下から押す力に対して変形しにくくなります。この効果を考慮した解析を行いま

• 本例題では圧電性のない材料を用いています。この様な解析は、応力解析の大変位解析をすることで正確に解析することができるのですが、振動の解析に展開するには過渡解析が必要になります。ここでは調和解析や共振解析に適用できる計算方法である「初期応力を考慮した解析」の機能を使用します。詳細は「初期応力を考慮した解析」を参照してください。。

• 初期応力（張力）を静解析の計算結果で指定する方法で解析します。

• 上の図にあるような、梁の両端を引っ張り、中央を押すという解析を、1/2モデルで解析します。解析方法は、次の通りです。
  解析①：張力の元となる静荷重を加え、左右に引っ張ります。
  解析②：梁の左右を固定し、下から押す力を加えたモデルを作成します。初期応力を考慮するため、解析①で得られた変位を使います。解析条件、結果インポートタブで解析モデル「解析①」を指定します。

解析空間（解析①、解析②共通）

解析条件（解析①）

モデル図（解析①）

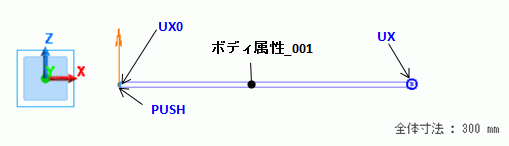
対称性を利用した1/2のモデルにしました。左端は対称の境界条件を設定、右端は、変位X成分=-0.1[mm]、ｙ成分、ｚ成分動かないという意味で、０[mm]を指定しました。

ボディ属性および材料定数の設定（解析①、解析②共通）

境界条件（解析①）

解析結果（解析①）

1/2モデルをそのまま表示しています。左端を固定、右端を右方向に引っ張った解析です。下の図は変位の大きさをコンター図で示していますが、最大値が１００[um]になりました。これは境界条件で設定したX方向変位の絶対値に等しい量です。

解析条件（解析②）

結果インポートタブを以下のように行います。

モデル図（解析②）

解析①と同様に1/2のモデルを解析します。解析①の変位分布を利用するので、同じ形状であることが必要です。1/2のモデルですので、左端に、対称の境界条件を設定しました。

形状は同じですが、境界条件を一部変更しています。右端は固定、左端に集中荷重の条件を加えています。

ボディ属性および材料定数の設定（解析②）

解析①と同じ

境界条件（解析②）

解析結果（解析②）

右端固定、左端を上向きに押していますので、予想通りの結果が得られました。ただし、この図だけでは、解析①の張力による影響が分かりません。

そこで、解析①の荷重を変えて、それが解析②の結果にどう影響するかを調べます。

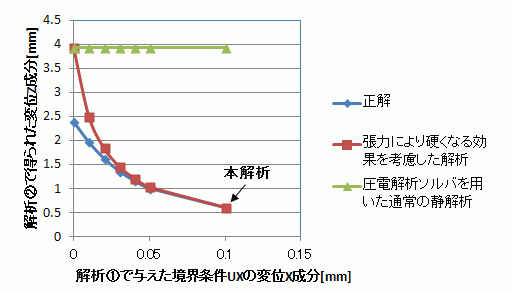
上図において、正解とあるのは、応力解析で大変位を考慮した解析の結果です。圧電解析ソルバを用いた通常の解析とは、解析①のX軸方向変位と、解析②のZ方向荷重を同時に加えた解析です。この計算方法では、張力による影響を全く考慮できていません。

張力により硬くなる効果を考慮した解析とは、本例題で紹介した方法ですが、図の左側では正解との差が大きいものの、右に行くに従って（張力が大きくなるにしたがって、）正解に近づくことが分かります。これは計算式の作成過程で、張力が支配的である、という仮定を導入した為です。