CAEソフト【 Femtet 】-ムラタソフトウェア株式会社

Thermoelastic Damping

本例題について
-
Thermoelastic Dampingを考慮した圧電共振解析を行い、Q値を求める。
-
結果として、温度分布、Q値を示す。
-
周波数の近似値は、Thermoelastic Damping OFFの共振解析で求めている。
(周波数の近似値について、このページの最後で説明しています。)
-
表に記載されていない条件は初期設定の条件を使用します。
解析条件
|
項目 |
条件 |
|
ソルバー |
圧電解析[Rayleigh] |
|
解析空間 |
2次元 |
|
解析の種類 |
共振解析 |
|
単位 |
mm |
|
解析オプション |
Themoelastic damping を考慮する |
共振解析タブ
|
タブ設定 |
設定項目 |
条件 |
|
共振解析 |
モード数 |
3 |
|
周波数の近似値 |
1.730×103[Hz] |
モデル図
長方形をZ方向に10個重ねた形状をしています。Z方向に変化する温度変化を少ないメッシュで、忠実に再現する為です。
横が20mmです。厚み(縦)は0.3mmですが、厚み方向を5倍にして表示していますので、実際より厚く見えます。

BODY属性および材料定数の設定
|
BODY No./BODY Type |
BODY名 |
材料名 |
|
n/Solid (0<=n<10) |
BEAM |
材料定数_001 |
BODY属性
|
BODY属性名 |
タブ |
解析領域 |
|
BEAM |
方向 |
指定方法:ベクトル ベクトル:X=Y=0.0、Z=1.0 |
|
|
厚み/幅 |
シートボディの厚み:1mm |
材料定数
|
材料名 |
タブ |
条件 |
|
材料定数_001 |
密度 |
7.8×103[Kg/m3] |
|
圧電定数タブ |
圧電性:なし 異方性:等方 ヤング率:2×1011[N/m2] |
|
|
比熱 |
2×103[J/kg/deg] |
|
|
熱伝導率 |
42[W/m/deg] |
|
|
線膨張係数 |
1.2×105[1/deg] |
境界条件
|
境界条件名/Topology |
タブ |
境界条件の種類 |
条件 |
|
FIX/Face |
機械 |
変位 |
UX=0, UY=0, UZ=0 |
解析結果
結果得られた温度分布を示します。異方性ズームの機能をつかって、縦方向に5倍伸ばして表示していますので、ご注意ください。

厚みを0.5mm~0.03mmの間で変更し、その時のQ値を複素共振周波数から次式を使って求めることができます。
Q値=共振周波数の実部/共振周波数の虚部/2
周波数の近似値は、Thermoelastic Damping OFFの共振解析で求めた値を用いました。TED解析における周波数の近似値の意味は、後で示します。
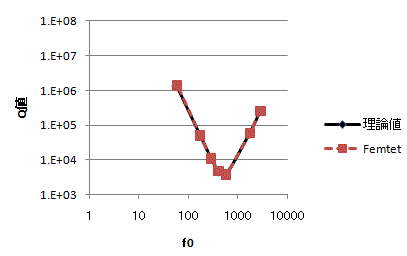
厚みを変えると、共振周波数とQ値が変わりますので、その関係を図示したのが、図1になります。理論式から求めたQ値とよく一致していることが分かります。
添付のプロジェクトファイルでは、厚み0.3を解析しています。プロジェクト内で定義された変数dzが、厚みの1/10になりますので、dzを変更することで、下に示した結果をトレースできます。
表1.厚みを変えた時のQ値の変化。
|
厚み[mm] |
参照周波数 [Hz] |
共振周波数 の実部[Hz] |
共振周波数 の虚部[Hz] |
Q値 |
|
0.5 |
2.877e3 |
2.878e3 |
5.578e-3 |
2.579e+5 |
|
0.3 |
1.728e3 |
1.728e3 |
1.462e-2 |
5.913e+4 |
|
0.1 |
5.764e2 |
5.765e2 |
7.488e-2 |
3.849e+3 |
|
0.07 |
4.035e2 |
4.035e2 |
4.204e-2 |
4.799e+3 |
|
0.05 |
2.882e2 |
2.882e2 |
1.296e-2 |
1.112e+4 |
|
0.03 |
1.728e2 |
1.728e2 |
1.726e-3 |
5.008e+4 |
図1.共振周波数の実部とQ値の関係を、Femtetの結果と理論計算値で比較
理論値の計算式

引用文献:H.Itoh JJAP 50 (2011) 087203
- 周波数の近似値の持つ意味について
Thermoelastic Dampingを考慮した解析において、周波数の近似値の持つ意味を説明します。Thermoelastic Dampingを考慮した共振解析では、次の式(1)を解く必要があります。この場合sは周波数、xが変位や温度といった分布を示すベクトル、A,B,Cはモデルの形状や材料定数を反映した行列です。しかし(1)を解くのは簡単でない為、それを簡単化した式(2)を使って、解析を行っています。srefとして、共振解析タブの”周波数の近似値”を利用しています。そのため、周波数の近似値は、結果として得られる共振周波数に近い値を使っていただく必要があります。
(A+sB+s2C)x=0 (1)
(A+srefB+s2C)x=0 (2)
まずはFemtetを試してみたい
試用版はこちらもっとFemtetについて詳しく知りたい
イベント・セミナー情報はこちら