浮き電極

本例題について

• 浮き電極の働きを簡単な例題をとおして確認します。

• 力で圧電体を変形させ、その時に発生する電位を確認します。

• 圧電定数との対応を確認します。

解析条件

モデル図

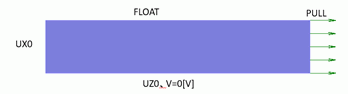
図のような直方体のソリッドボディを定義し、各面に境界条件を与えています。

ボディ属性および材料の設定

※材料データベースを利用

境界条件

解析結果

下図(a)は応力分布を示しています。ｘ軸方向に1[Pa]の応力が発生していることがわかります。荷重として1[Pa]の面荷重を与えたので、発生した応力になります。

この応力により発生する電界を、Ｄ形式の圧電方程式を使って考えます。

D=dT+εE        (1)

応力はX成分のTxのみが存在します。応力X成分に関係する圧電D定数で０以外の値を持つのはd31になります。つまりDZ成分の存在する可能性があるわけですが、浮き電極があって、その電荷は０ですので、DZ=0になります。

つまり(1)式より、　０＝d31・Tx＋εz・Ez  が成り立ちます。応力（Tx)をこの式にいれると、電界Ezが得られます。この解析で用いた材料000P-4ではd31=-0.7e-11[C/N]、εz＝200ε0、です。

Ez＝-d31・Tx/εz=-(-0.7e-11)・1.0/（200・8.854e-12)=3.953e-3　[V/m]　　　(2)

下図(b)は、Femtet(R)で計算した電界になります。(2)式で得られた電界と一致しています。圧電体の中の電界は一定ですので、電位差は、Ezに厚みをかけることで求めることができます。

下図(c)は、得られた電位分布です。