Example5 Transient Analysis of Flow around Cylinder

General

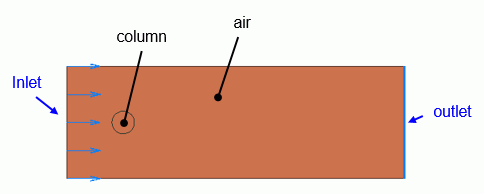
• The flow around the cylinder is analyzed.
   

• The flow velocity distribution, the fluid velocity vectors, the streamlines, the vorticity, and the force on the wall face are solved.
   

• Unless specified in the list below, the default conditions are applied.
   

Analysis Space

Analysis Conditions

Model

The material of Air (000_Air) is set to a rectangular sheet body. The boundary conditions of inlet and outlet are set on the left edge and the right edge respectively.

The slip wall outer boundary condition is applied to the top and bottom edges where the boundary condition is not set.

The model is a circle sheet body and the material is iron (007_Fe).

The edges surrounding a circle is a boundary of solid and fluid. Solid wall is automatically set to them.

Body Attributes and Materials

* Available from the material DB

Boundary Condition

If Reynolds number exceeds 100, the time dependency of the turbulence occurs. It makes calculation difficult in the steady-state analysis.

The Reynolds number calculated with this model form, material property, and flow velocity is about 126.0. Use transient analysis instead.

Viscosity μ=1.816e-5[Pa s]

Density ρ=1.144[kg/m3]

Kinematic viscosity v=μ/ρ=1.816e-5/1.144=1.587e-5[m2/s]

Flow velocity V=0.05[m/s]

Diameter of cylinder D=0.04[m]

Reynolds number Re = V*L/ν=0.05*0.04/1.587e-5 = 126.0

Results

The vectors of the flow velocity distribution around the cylinder at time 48[s] and 50[s] are shown below.

The vectors are adjusted to the same length in the graphics setup.

It is known that at a Reynolds number of 126, the Karman vortices are shed from the alternating sides of the cylinder.
In the diagram below, a vortex appears on the upper side of the cylinder at 48[s] and the lower side at 50[s].

48[s]
50[s]

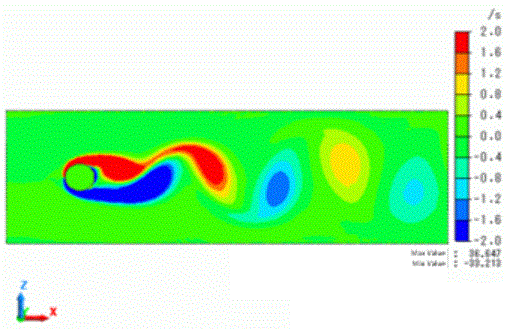
The figure below is the contour of Y component of the vortex at 50[s]. The scale is minimum: -2[/s] and maximum: 2[/s].

The vortex strength in the Y direction is shown. The clockwise vortices are shown in the positive value, and the counter-clockwise vortices in the negative value.

You can observe the vortices are shed downstream from the cylinder.

The force on the wall face is shown by the table.

[column] represents the force which the cylinder receives from the fluid.

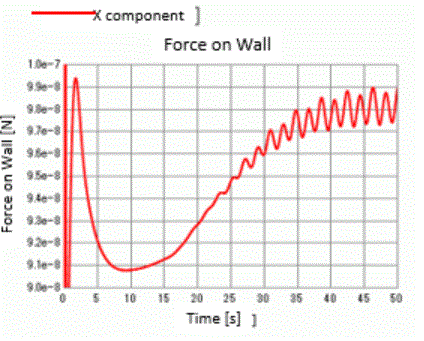
The result below shows only column/X component (drag F: force in the flowing direction).

(Double click the graph to show the plot option. Deselect [Display Y-axis (primary axis)] except column/X component. Change the color of column/X component to red.)

The range of the scale for the vertical axis is changed to 0.9 x 10^-7 ～1.0 x 10^-7.

The drag force near time 50[s] fluctuates centering around 9.8 x 10^-8[N] at a cycle of about 2[s].

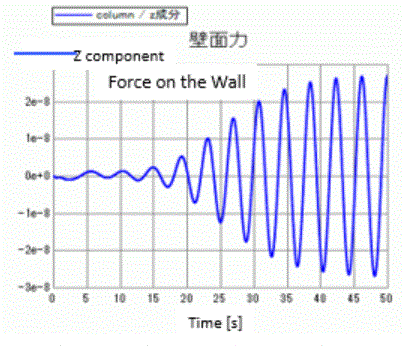
The result below shows only column/Z component (lift: force in the direction perpendicular to the flow).

(Double click the graph to show the plot option. Deselect [Display Y-axis (primary axis)] except column/X component. Change the color of column/X component to blue.)

You can see that the lift is fluctuating at a constant cycle of about 4 [s].

The drag coefficient CD can be calculated from the drag F.

Thickness in depth direction t = 1[mm]

Cross sectional area S = D * t = 0.04 * 0.001 = 4e-5 [m2]

Dynamic pressure Pk = 0.5 * ρ*V^2 = 0.5 * 1.144 * 0.05 * 0.05 = 1.430e-3 [Pa]

Drag coefficient (CD) = F / Pk / S = 9.8e-8 / 1.430e-5 /4e-5 = 1.71