CAE Software【Femtet】Murata Software Co., Ltd.

Example36 Damping Vibration of Cantilever
General
-
A cantilever is mechanically loaded. After it is unloaded, it starts to vibrate. The vibrations decays over time.
-
The displacement and the mechanical stress are solved for each time step.
-
Unless specified in the list below, the default conditions will be applied.
Analysis Space
|
Item |
Settings |
|
Analysis Space |
3D |
|
Model unit |
mm |
Analysis Conditions
|
Item |
Settings |
|
Solvers |
Mechanical Stress Analysis [Galileo] |
|
Analysis Type |
Transient analysis |
The transient analysis is set up as follows.
|
Tab |
Setting Item |
Settings |
|||||||||
|
Transient Analysis Tab |
Table |
|
|||||||||
|
Rayleigh Damping Coefficients |
Beta=0.0002 |
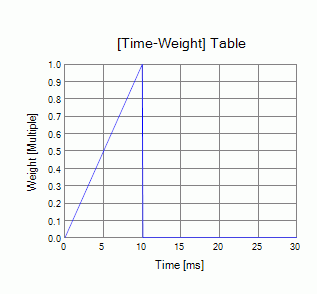
The load gradually increases in the first 5 steps. In the next 100 steps,
it is unloaded, and the damping vibration occurs.
0 – 0.01 [sec]: Loading period
0.01 – 0.03 [sec]: Vibration period
Model
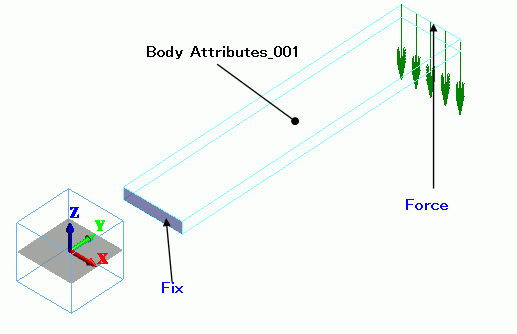
Body Attributes and Materials
|
Body Number/Type |
Body Attribute Name |
Material Name |
|
0/Sheet |
Body_Attribute_001 |
002_Polycarbonate(PC) |
Boundary Conditions
|
Boundary Condition Name/Topology |
Tab |
Boundary Condition Type |
Settings |
||||||||||
|
Fix/Face |
Mechanical |
Displacement |
Select all X/Y/Z components. UX=0, UY=0, UZ=0 |
||||||||||
|
Force/Face |
Mechanical |
Distributed face load |
X=0, Y=0, Z=-0.5×10^5
Time Dependency: Yes
The loading is removed instantaneously at 0.01[sec]. |
Tips on Analysis Conditions and Boundary Conditions
Perform a static analysis and obtain the adequate loading condition for the target displacement beforehand.
Perform a resonant analysis and obtain the adequate time steps for the expected vibration period.
Results
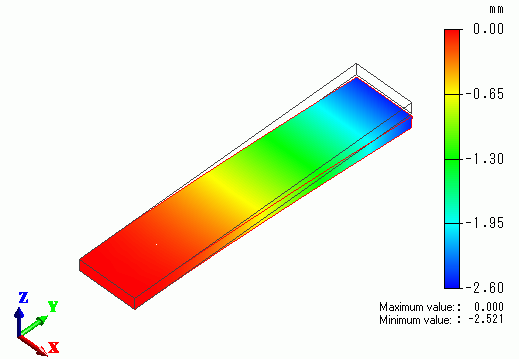
The displacement diagram below shows the deformation at 0.01[sec] (Mode number 5). The color gradation contour indicates the Z displacement.
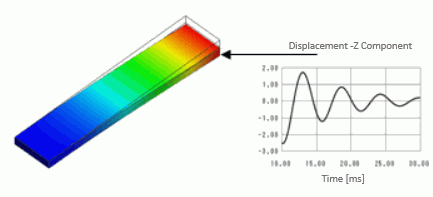
Plotted below is the Z displacement of the cantilever tip in 0.01 to 0.03 [sec] (Mode numbers 5 through 105)
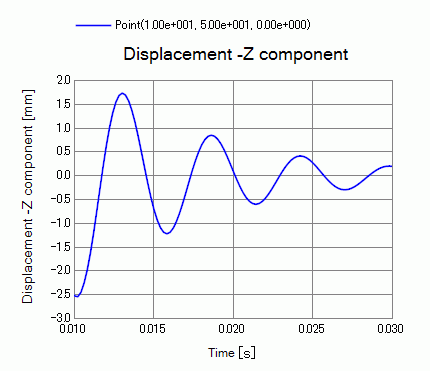
The vibration decays as the time passes.
The figure below shows the vibration when Beta is set to 0.
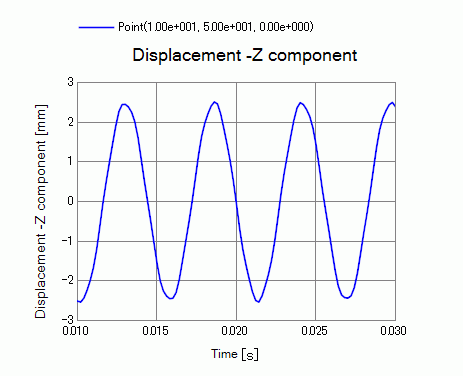
There is no decay.