Example42 Mechanical Stress of Rod Inserted into Ring

General

• A rod is inserted into a ring. The outer diameter of the rod is slightly larger than the inner diameter of the ring.
   

• Ring’s outer diameter, d2 = 50mm, Ring’s inner diameter after insertion, d1 = 40mm
  The difference between the rod’s outer diameter and the ring’s inner diameter is 0.2mm.
   

• The distributions of displacement and mechanical stress are solved.
   

• Unless specified in the list below, the default conditions will be applied.
   

Analysis Space

Analysis Conditions

 Model

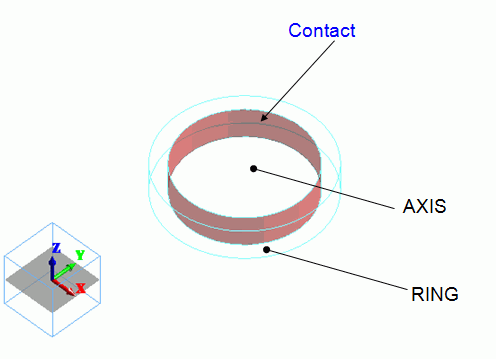
Two cylindrical solid bodies are created. The smaller cylinder is subtracted from the larger cylinder with boolean.
The larger one becomes the ring, and the smaller one becomes the rod.

The inner face of the ring is set with the simple contact boundary condition.

Body Attributes and Materials

* Available from the Material DB

Taking into account the diameter change, AXIS is set with the initial strain of 0.005, which comes from 0.2[mm] / 40[mm].

Boundary Conditions

RING and AXIS are not adhered. They are in simple contact.

Results

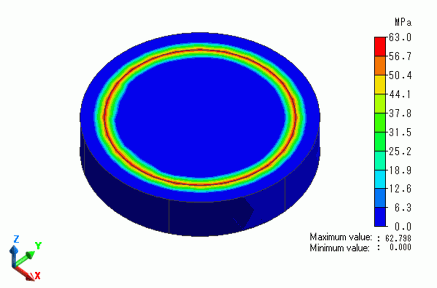
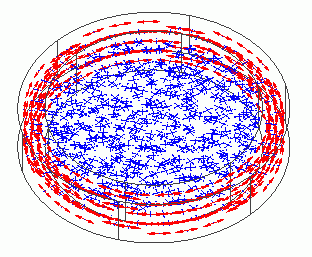
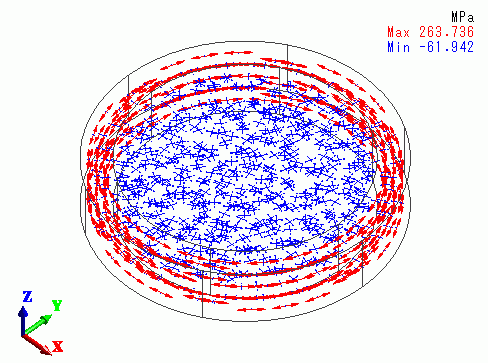
The vectors of the mechanical stress are shown below.

The ring gets tensile stress circumferentially, while the rod gets compressive stress radially.

Theoretically, the pressure at the contact face, P, is given by the following.

P = Eδ(d2^2 – d1^2 ) / (d1 * d2^2)

E is Young’s modulus [Pa], δ is the fitting differential [m], d2 is Ring’s outer diameter [m], and d1 is Ring’s inner diameter [m].

For this particular model,

P = 6.85 x 10^10 * 0.1 * ( 50^2 – 40^2 ) / ( 40 * 50^2)

= 6.165 x 10^7

The contour below shows the magnitude of pressure at the contact face.

This is close to the theoretical value, 6.165 x 10^7[Pa].