
CAE Software【Femtet】Murata Software Co., Ltd.

Example48 Buckling Analysis

General
-
The buckling analysis is performed for an H-beam steel.
-
The object’s buckling load factor and the buckling modes are solved.
-
Unless specified in the list below, the default conditions will be applied.
Analysis Space
|
Item |
Settings |
|
Analysis Space |
3D |
|
Model unit |
mm |
Analysis Conditions
The analysis type is buckling analysis
|
Item |
Settings |
|
Solvers |
Mechanical Stress Analysis [Galileo] |
|
Analysis Type |
Buckling analysis |
Model
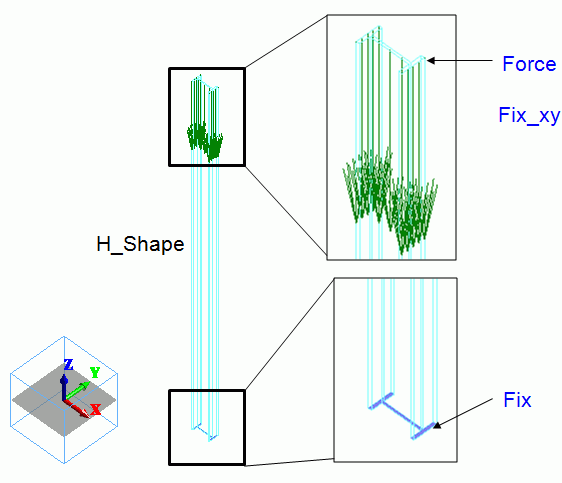
An H-shaped sheet body is created on XY plane. It is extruded to form an H-shape pillar.
The bottom face is fixed. The top face is loaded downward and fixed in X and Y directions. Uniform displacement is set on it.*
* The uniform displacement prevents the rotational displacement.
Body Attributes and Materials
|
Body Number/Type |
Body Attribute Name |
Material Name |
|
0/Solid |
H_shape |
104_Stainless_steel * |
* Available from the Material DB
Boundary Conditions
|
Boundary Condition Name/Topology |
Tab |
Boundary Condition Type |
Settings |
|
Fix/Face |
Mechanical |
Displacement |
Select all X/Y/Z components. UX=0, UY=0, UZ=0 |
|
Force/Face |
Mechanical |
Load |
Select “Set the total load”. X=0.0, Y=0.0, Z=-1000 |
|
Fix_xy/Face |
Mechanical |
Displacement |
Select X and Y components. UX=0, UY=0 Select “Uniform displacement” |
Results
The following will be output on the Output Window or the log file.
|
<<Buckling Analysis>> Buckling load factor Mode[ 0] = 2.88264161e+002
Multiply the original load with the buckling load factor to acquire the buckling load. Field values such as displacement, strain, stress, etc acquired by the buckling analysis are all relative. |
In this model, the buckling load factor is 288.
The load set on “Force” is 1000[N]. Therefore, the buckling load is 288[KN]
The displace diagram is shown below. The contour diagram shows the displacement. The displacement is relative.

Compare with Theoretical Values
The buckling load for a H-shape pillar is given by the following formula.
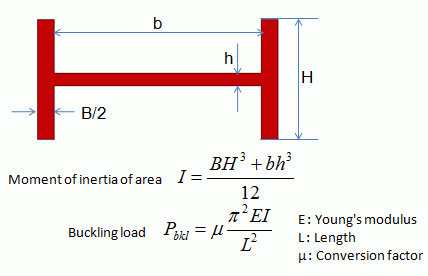
In this case,
B/2 = 7e-3[m]
b = 86e-3[m]
H = 50e-3[m]
h = 5e-3[m]
E = 2e11[Pa]
L = 2.0[m]
μ=4, which means that there is no horizontal or rotational displacement for either end.
These values yield I = 14.7e-8[m4] and Pbkl = 290[KN]
The result of Femtet matches this Pbkl quite well.

