Example17 Temperature-Dependent Heat Source (Transient Analysis)

General

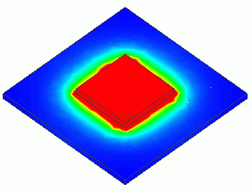
• The model is the same as Exercise 8: A heat source is placed on a substrate, and there is a forced air flow for cooling in parallel to the substrate. The heat radiation is analyzed under the transient condition.
  The heat source is temperature-dependent.
   

• The heat transfer coefficient is acquired manually.
  To acquire it automatically, see “Ex.1 of Simple Fluid-Thermal Analysis”.
   

• The temperature distribution and the heat flux vectors are solved.
   

• Unless specified in the list below, the default conditions will be applied.
   

Analysis Space

Analysis Conditions

The transient analysis is set up in transient tab as follows. The total number of steps is 20. The time step is 30 second.

Therefore, the temperature distributions for 600 seconds are solved.

Model

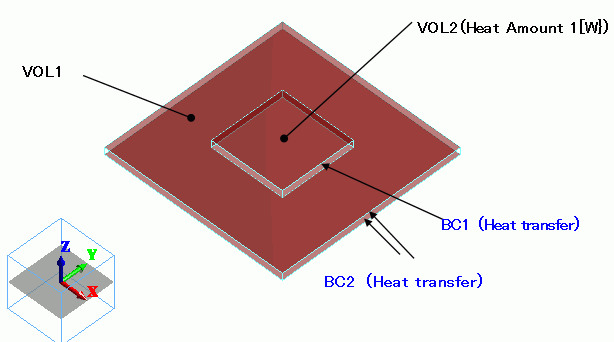
The same as Exercise 7. The material properties and the boundary conditions are the same as well.

The substrate (VOL1) and the heat source (VOL2) are created as solid body box, and the heat source is defined in the body attribute of VOL2.

The heat transfer coefficients for the top and bottom faces of the substrate and the top face of the heat source are calculated based on the simplified equation.

Body Attributes and Materials

* Available from the Material DB

The heat source of VOL2 is set up as follows.

Heat source is specified by heat density in the analyses where temperature-dependent heating materials are involved.

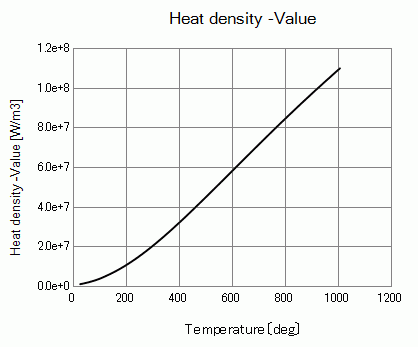
On Exercise 8, we set 1[w] for the heat source of VOL2. As the volume of VOL2 is 800*10^-9[m^3], the heat density is equal to

1.25 x 10^6 [W/m^3].

This is the value for 25[deg], so

P(25) = 1.25 x 10^6 [W/m^3]

in the Arrhenius equation which is given by the following:

P(T) = 1.25 x 10^6 * exp(-0.15/(k*(T+273))) / exp (-0.15/(k*(25+273)))

where 0.15[eV] is the activation energy and k is the Boltzmann constant.

Heat density’s temperature plot is shown below.

Boundary Conditions

The heat transfer coefficients for the forced convection are calculated as follows. The equation is given in Exercise 8: Heat Radiation by Forced Convection (Transient Analysis).

For the details, please refer to the Heat Transfer Coefficient for Forced Convection

To acquire it automatically, see “Ex.1 of Simple Fluid-Thermal Analysis”.
 

Results

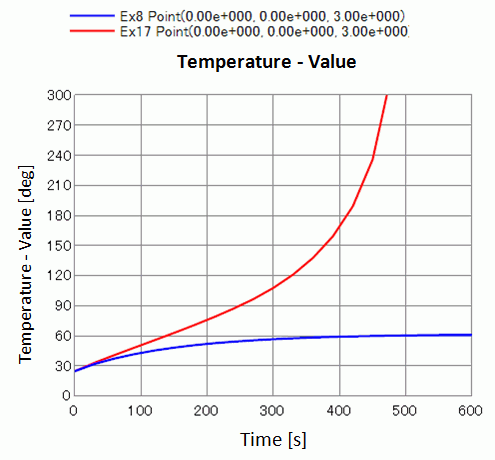
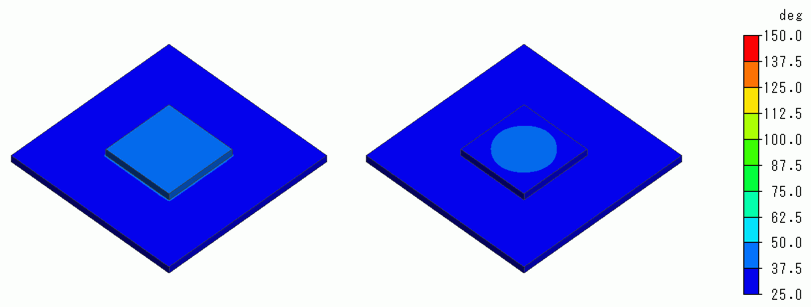
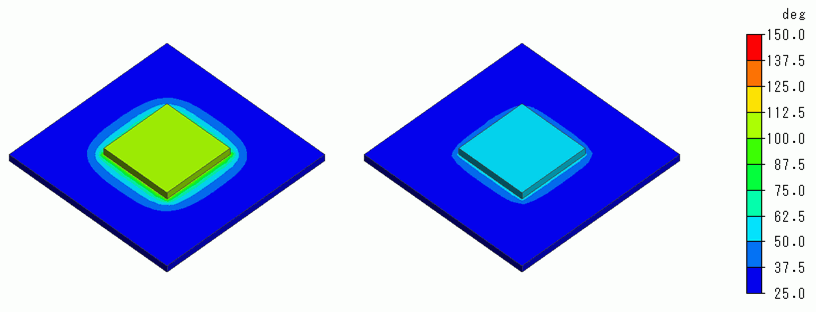
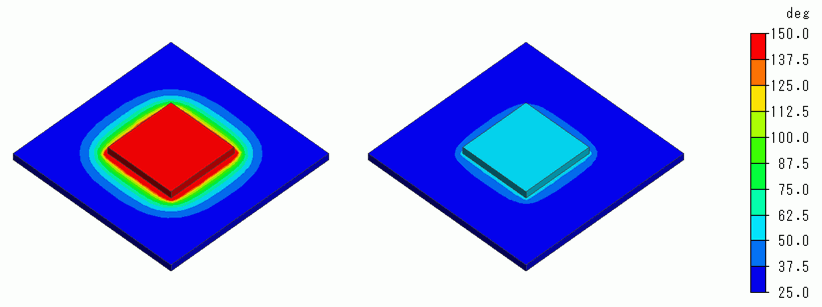
The temperature distributions for Exercise 8 (right figures) and this exercise (left figures) are shown below for the elapsed time of 60, 300 and 600 seconds.

The unit of the color scale is [deg].

At Minimum/Maximum Value on the Contour tab of [Graphics Setup], deselect “Automatic” and set 25 => 150.

There is almost no difference in 60 seconds.

However, it becomes obvious that the temperature increases much higher than Exercise 8 in 300 and 450 seconds.

In 60 seconds

In 300 seconds

In 450 seconds

The temperature vs. time is plotted below.