
CAE Software【Femtet】Murata Software Co., Ltd.

Example12 Resonance of Metal Bars
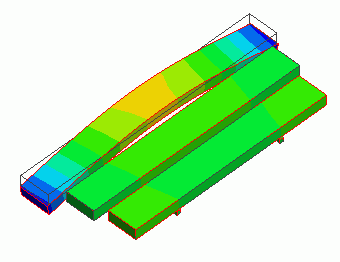
General
-
The resonance of three metal bars is analyzed.
-
The deformation, the displacement and the mechanical stress are solved.
-
Unless specified in the list below, the default conditions will be applied.
Analysis Space
|
Item |
Settings |
|
Analysis Space |
3D |
|
Model unit |
m |
Analysis Conditions
The analysis type is the harmonic analysis.
|
Item |
Settings |
|
Solvers |
Mechanical Stress Analysis [Galileo] |
|
Analysis Type |
Resonant analysis |
|
Options |
N/A |
The resonant analysis tab is set up as follows.
|
Tab |
Setting Item |
Settings |
|
Resonant analysis |
Number of modes |
6 |
|
Approximated frequency |
0[Hz] |
Model
Three metal bars and two support rods are created as box-shape solid body.
The bottom faces of support rods are fixed with the displacement boundary condition.
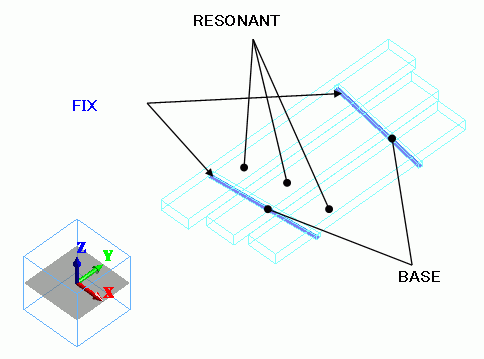
Body Attributes and Materials
|
Body Number/Type |
Body Attribute Name |
Material Name |
|
0/Solid |
RESONANT |
001_Al * |
|
1/Solid |
RESONANT |
001_Al * |
|
2/Solid |
RESONANT |
001_Al * |
|
8/Solid |
BASE |
M_BASE |
|
9/Solid |
BASE |
M_BASE |
* Available from the Material DB
The material properties are set up as follows:
|
Material Name |
Tab |
Properties |
|
M_BASE |
Elasticity |
Young’s modulus: 2×10^9[Pa] Poisson’s ratio: 0.3 |
|
Density |
Density: 0.1×10^3[Kg/m3] |
Boundary Conditions
The bottom faces of support rods are fixed with the displacement boundary condition.
|
Boundary Condition Name/Topology |
Tab |
Boundary Condition Type |
Settings |
|
FIX/Face |
Mechanical |
Displacement |
Select all X/Y/Z components. UX=0, UY=0, UZ=0 |
Results
The following will be output on the output window.
|
<<Eigenvalue analysis>> Eigenvalue (resonant frequency):[Hz] Mode[ 0] = 8.61552809e+002 Mode[ 1] = 1.06874655e+003 Mode[ 2] = 1.21598202e+003 Mode[ 3] = 1.24695787e+003 Mode[ 4] = 1.56876049e+003 Mode[ 5] = 1.69339225e+003 |
The resonant frequencies can be checked on Table.
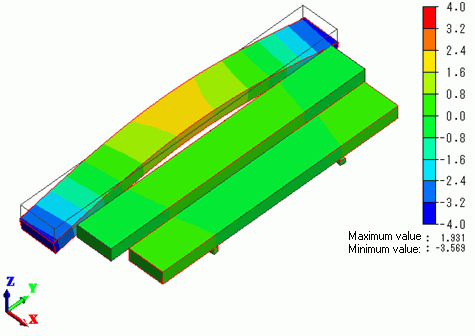
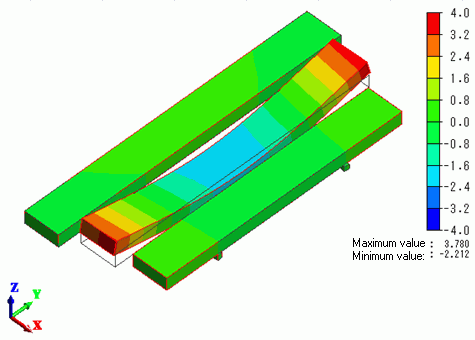
The displacement diagrams of Mode[0] to Mode[ 2] are shown below.
The contour are the Z displacement.
The minimum and maximum values are manually set to
-4.000e+000 and 4.000e+000 respectively.
Mode[0]:8.615528e+002[Hz]
Mode[1]:1.068747e+003[Hz]
Mode[2]: 1.215982e+003[Hz]
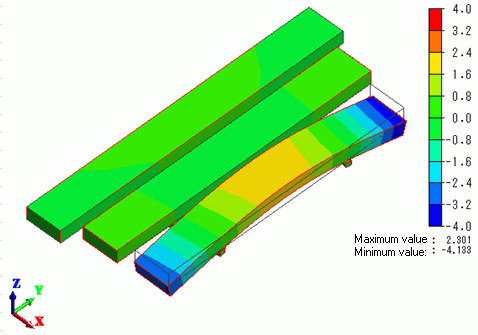
The shorter bar exhibits the higher resonant frequency.

