
CAE Software【Femtet】Murata Software Co., Ltd.

Example27 Current Induced in Wire-Wound Inductor
General
-
The current induced in a wire-wound Inductor is analyzed.
-
The current distribution and the resistance are solved.
-
This will be an axisymmetric analysis.
-
Unless specified in the list below, the default conditions will be applied.
Analysis Space
|
Item |
Settings |
|
Analysis Space |
Axisymmetric |
|
Model unit |
mm |
Analysis Conditions
|
Item |
Settings |
|
Solvers |
Magnetic Field Analysis [Gauss] |
|
Analysis Type |
Harmonic analysis |
|
Options |
Deselect Inductance Calculation. |
The frequency is swept from 1MHz to 10MHz in 1MHz interval.
|
Tab |
Setting Item |
Settings |
|
Harmonic analysis |
Frequency |
Minimum: 1×10^6[Hz] Maximum: 10×10^6[Hz] |
|
Step |
Linear step: Division number: 9 |
Model
The axisymmetric analysis is performed. For a model which is symmetric around Z axis,
the simulation is done for the X-Z section only. It is virtually 2D analysis.
The calculation is much faster than 3D analysis. The axisymmetric analysis is well suited for this exercise.
A core is placed in center, and the coil is wound on the core.
The coil is formed by 16 turns in Z direction and 4 layers in X direction. It is 64 turns in total.
The right half section of the model is analyzed.
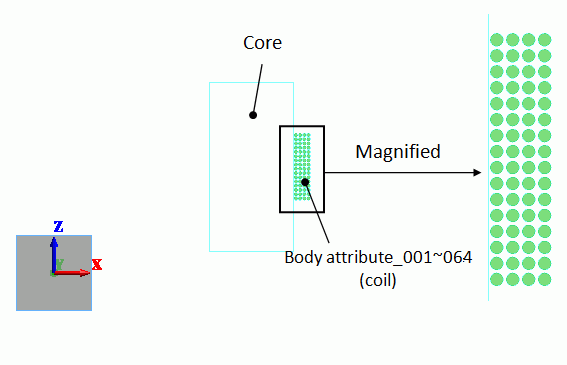
Body Attributes and Materials
|
Body Number/Type |
Body Attribute Name |
Material Name |
Mesh Size |
|
0-63/Sheet 65/Sheet |
Body_Attribute_001 to 064 CORE |
008_Cu * CORE |
0.01
|
* Available from the Material DB
Set the current as follows.
|
Body Attribute Name |
Tab |
Settings |
|
Body_Attribute_001 to 064 |
Current |
Waveform: AC Current: 1[A] Turns: 1[Turns] Direction: +Y direction |
Boundary Conditions
No setting.
Results
The following are solved.
1) Magnetic flux lines
2) Current density distribution
3) Frequency characteristics of the inductor’s resistance
4) Inductance
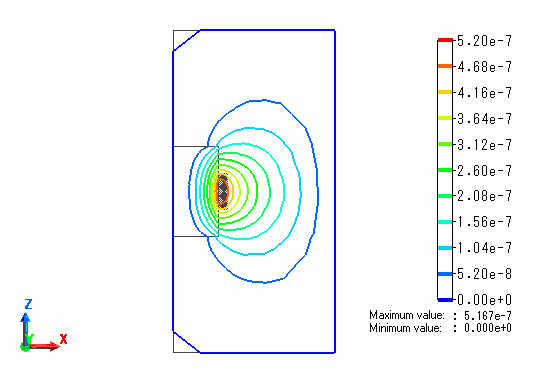
1) Magnetic flux lines
The figure below shows the magnetic flux lines at 10MHz.
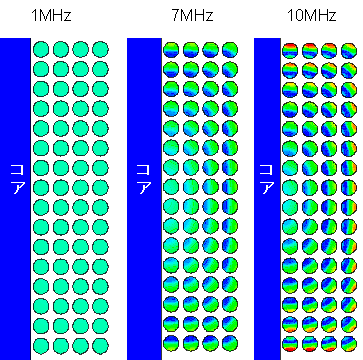
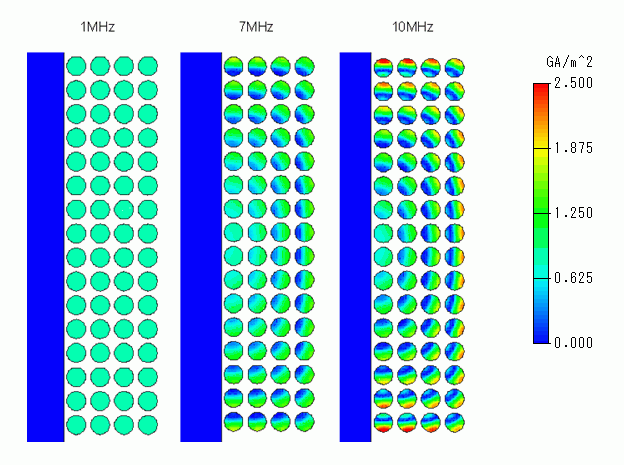
2) Current density distribution
The figure below shows the current distribution. The current flows uniformly at 1MHz. At higher frequencies, the current flows unevenly especially in the outer windings.
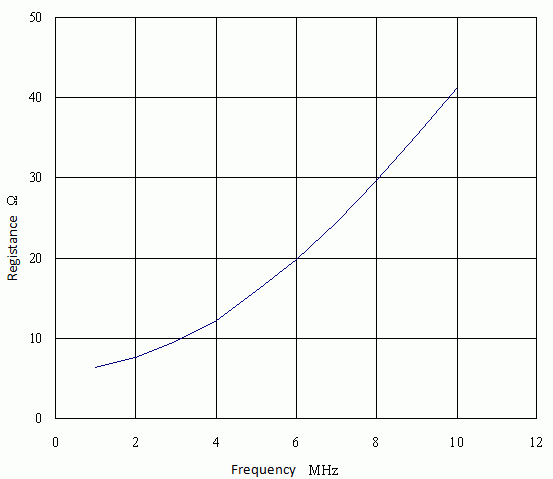
3) Frequency characteristics of the inductor’s resistance
The chart below is the inductor’s resistance. It is higher at higher frequency.
-
How to calculate the resistance
Resistance R can be calculated from the loss P [W] displayed on the output window:
R = 2*P, where P = 1/2*R*I*I and I = 1[A] peak.
4) Inductance
The inductance can be calculated as follows. The magnetic energy Em, the current I and the inductance L satisfy
Em = 1/2*L*I*I As Em = 1.563e-5[J] is obtained at I = 1[A] through the simulation,
L = 31.26[uH]

