Example7 Model with Reflective Symmetry

General

A quarter model of Exercise 2 is analyzed with reflective symmetry applied.
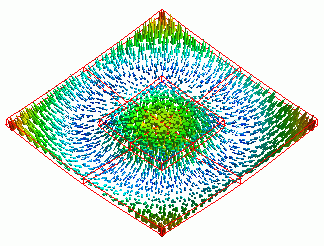
The figure above is obtained with [Full Model].
The reflective symmetry is used as boundary condition.

The temperature gradient caused by the heating chip is calculated by thermal analysis [Watt].
The result is passed on to Galileo as a thermal load.
The deformation, the displacement and the mechanical stress are solved.
Unless specified in the list below, the default conditions will be applied.

Analysis Space

Item	Settings
Analysis Space	3D
Model unit	mm

Analysis Conditions

Select Thermal analysis and Mechanical stress analysis.

Item	Settings
Solver	Thermal Analysis [Watt] Mechanical Stress Analysis [Galileo]
Thermal-Analysis Type	Steady-State Analysis
Options	N/A *

* “Thermal Load” is selected by default for the thermal load-mechanical stress coupled analysis.

The Step/Thermal Load tab is set as follows.

Tabs	Setting Item	Settings
Step/Thermal Load *	Reference temperature	25[deg]

* The reached temperatures come from the thermal analysis.

Model

This is a quarter model of Exercise 2.

The planes of symmetry are YX and ZX planes.

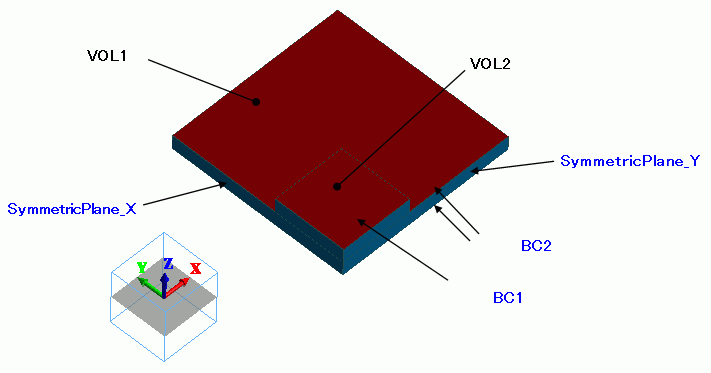
Body Attributes and Materials

Body Number/Type	Body Attribute Name	Material Name
0/Solid	VOL1	006_Glass_epoxy *
1/Solid	VOL2	001_Alumina *

* Available from the Material DB

As for the heat source of VOL2

enter 0.25[W] which is a quarter of the original model.

Body Attribute Name	Tab	Setting
VOL2	Heat Source	0.25[W]

Boundary Conditions

Set reflective symmetry on the applicable topologies.

Boundary Condition Name/Topology	Tab	Boundary Condition Type	Settings
SymmetricPlane_X/Face	Symmetry/Continuity	Symmetry	Reflective
SymmetricPlane_Y/Face	Symmetry/Continuity	Symmetry	Reflective

The heat transfer coefficients for the forced convection are calculated as follows. See [Heat Transfer/Ambient Radiation] for more information.

h = 3.86 x (V/L)0.5xC [W/m2/deg]

where

Air flow V=1[m/s]

Top and bottom faces of the substrate (VOL1): Characteristic length L=0.05, C=1 -> h=17.26
Top face of the heat source (VOL2): Characteristic length L=0.02, L’=0.015, C=1 * -> h=27.3

The thickness (d) of the speed boundary layer at the edges of the heat source is given by

d=0.0182x(L’/V)0.5= 2.3[mm]

This is close enough to the thickness of heat source, so we set C=1.

Boundary Condition Name/Topology

Tab

Boundary Condition Type

Settings

BC1/Face

Thermal

Heat Transfer/Ambient Radiation

Heat transfer coefficient: 17.26[W/m2/deg]

Room temperature: 25[deg]

BC2/Face

Thermal

Heat Transfer/Ambient Radiation

Heat transfer coefficient: 27.3[W/m2/deg]

Room temperature: 25[deg]

Thermal analysis is performed based on the boundary conditions below. The resulting temperature distribution is forwarded to mechanical stress analysis.

Results

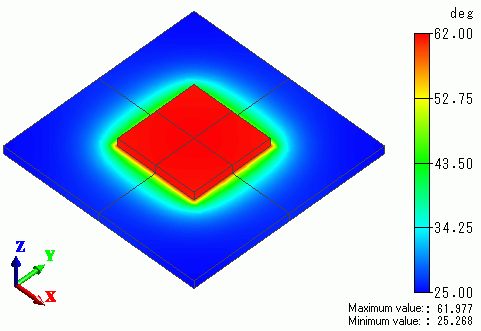
The temperature distribution as a result of Watt is shown below.

The next figure shows the vectors of displacement as a result of Galileo following Watt.

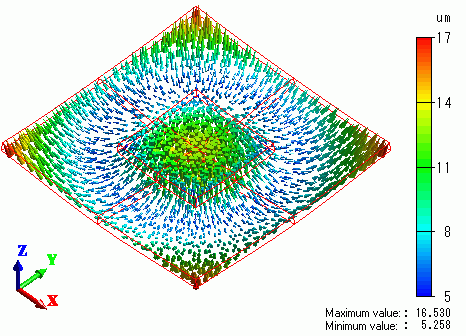
They are quite similar to the results of Exercise 2.